
【题目】如图所示,已知□ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
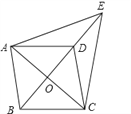
(1)四边形ABCD是菱形吗?请说明理由;
(2)若∠AED=2∠EAD,试说明四边形ABCD是正方形.
【答案】(1)四边形ABCD是菱形,理由见解析;(2)理由见解析.
【解析】分析:(1)根据对角线互相垂直的平行四边形是菱形.∵△ACE是等边三角形,∴EO⊥AC(三线合一),即AC⊥BD.∴四边形ABCD是菱形;
(2)根据有一个角是90°的菱形是正方形.由题意易得∠DAO=∠ADO=∠DAE+∠DEA=15°+30°=45°,∵四边形ABCD是菱形,∴∠DAB=2∠ADO=90°,∴四边形ABCD是正方形.
解:(1)四边形ABCD是菱形,理由如下:
∵四边形ABCD是平行四边形 ∴OA=OC,即O是AC的中点.
∵△ACE是等边三角形. ∴OE⊥AC, ∴BD⊥AC, ∴□ABCD是菱形;
(2)∵四边形ABCD是平行四边形, ∴AO=CO
∵△ACE是等边三角形 ∴∠AEC=∠EAC=60°,∠AED=30°,
∵∠AED=2∠EAD, ∴∠EAD=15° ∴∠DAO=∠ADO=45°,
∵四边形ABCD是菱形; ∴∠DAB=90° ∴四边形ABCD是正方形.
点睛: 此题主要考查菱形和正方形的判定,要灵活应用判定定理及等腰三角形的性质、外角的性质定理:对角线互相垂直的平行四边形是菱形;有一个角是直角的菱形是正方形;三角形的一个外角等于和它不相邻的两内角之和.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
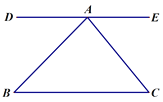
【题目】如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,
(1)求∠DAB的度数,并写出理由.
(2)求∠EAC的度数.
(3)计算∠BAC的度数.
(4)根据以上条件及结论,你还能得出其他结论吗?试写出一个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(2m–2)x+m+1 (1)、m为何值时,图象过原点.(2)、已知y随x增大而增大,求m的取值范围.(3)、函数图象与y轴交点在x轴上方,求m取值范围.(4)、图象过二、一、四象限,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,BC是⊙O的直径,点A在⊙O上,点D在CA的延长线上,DE⊥BC,垂足为点E,DE与⊙O相交于点H,与AB相交于点l,过点A作⊙O的切线AF,与DE相交于点F.
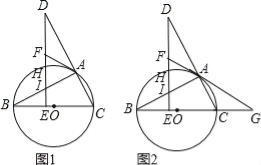
(1)求证:∠DAF=∠ABO;
(2)当AB=AD时,求证:BC=2AF;
(3)如图2,在(2)的条件下,延长FA,BC相交于点G,若tan∠DAF=![]() ,EH=2
,EH=2![]() ,求线段CG的长.
,求线段CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有红、白、黄3种颜色的若干个小球,它们除颜色外完全相同.每次从袋中摸出1个球,记下颜色后放回搅匀再摸.摸球实验中,统计得到下表中的数据:
摸球次数 | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
出现红球的频数 | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
出现白球的频数 | 1 | 4 | 16 | 36 | 52 | 61 | 75 | 85 | 123 | 151 |
由此可以估计摸到黄球的概率约为________(精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕,某校为学生购买了A、B两种品牌的粽子共400个,已知B品牌粽子的单价比A品牌粽子的单价的2倍少6元.
(1)当买A品牌100个,B品牌粽子300个时,学校所花费用为4500元.求A、B两种品牌粽子各自的单价;
(2)在两种品牌粽子单价不变的情况下,由于资金临时出现状况,所花费用不超过4000元,问至少买A品牌粽子多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com