考点:待定系数法求二次函数解析式,待定系数法求一次函数解析式,二次函数图象上点的坐标特征
专题:
分析:(1)由图可得点A,C,B的坐标,设抛物线的解析式为y=ax2+bx+c,把A(3,0),B(-1,0),C(0,3)代入得出方程组,求解即可得出抛物线的解析式,设直线AB的解析式为y=kx+b,把A(3,0),B(0,3)代入可得方程组,求解即可得出直线的解析式,
(2)当直线平行与直线AB,且与抛物线只有一个交点时,S△AMB的最值.设直线为y=-x+b,可得-x+b=-x2+2x+3,利用△=0解得b的值,利用图形可得出BD的值,再由∠ODM=45°,BM⊥DM,可得BM的值,利用三角形面积公式即可求出S△AMB.
解答:解:(1)由图可得A(3,0),C(-1,0),B(0,3),
设抛物线的解析式为y=ax
2+bx+c,
把A(3,0),B(-1,0),C(0,3)代入可得
,解得
,
所以抛物线的解析式为y=-x
2+2x+3,
设直线AB的解析式为y=kx+b,
把A(3,0),B(0,3)代入得
,解得
,
所以y=-x+3,
(2)当直线平行与直线AB,且与抛物线只有一个交点时,S
△AMB的最值.
设直线为y=-x+b,
可得-x+b=-x
2+2x+3,化简得,x
2-3x+b-3=0,
由△=0可得9-4×(b-3)=0,解得b=
,
如图,BD=b-OB=
-3=
,
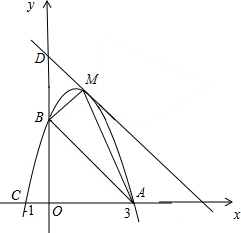
∵∠ODM=45°,
∴BM⊥DM,
∴BM=
,
∴S
△AMB=
×3
×
=
.
点评:本题主要考查了用待定系数法求二次函数及一次函数,图象上坐标点的特征等,解题的关键是利用△求出b的值.

 如图:
如图:


 发散思维新课堂系列答案
发散思维新课堂系列答案 如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的点落在点O处),把这个正六边形的面积n等份,那么n的所有可能取值的个数是( )
如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的点落在点O处),把这个正六边形的面积n等份,那么n的所有可能取值的个数是( ) 如图,AB是半圆O的直径,C为半圆上一点,过C作半圆的切线,连接AC,作直线AD,使∠DAC=∠CAB,AD交半圆于E,交过C点的切线于点D.
如图,AB是半圆O的直径,C为半圆上一点,过C作半圆的切线,连接AC,作直线AD,使∠DAC=∠CAB,AD交半圆于E,交过C点的切线于点D.