
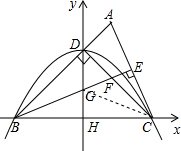
 (2011•南岸区一模)如图,△ABC中,AB=BC=2,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G.以点H为原点,BC所在直线为x轴建立如图所示的平面直角坐标系.
(2011•南岸区一模)如图,△ABC中,AB=BC=2,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G.以点H为原点,BC所在直线为x轴建立如图所示的平面直角坐标系.| 2 |
| 1 |
| 2 |
 (2)线段BG与CE之间存在数量关系BG=
(2)线段BG与CE之间存在数量关系BG=| 2 |
| CE |
| sin∠CGE |
| CE |
| sin45° |
| 2 |
| 2 |


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
 (2011•南岸区一模)如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个n×n的正方形图案(如图②③④…),其中图②中完整的圆共有5个,图③中完整的圆共有13个,…,若这样铺成一个10×10的正方形图案,则其中完整的圆共有( )
(2011•南岸区一模)如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个n×n的正方形图案(如图②③④…),其中图②中完整的圆共有5个,图③中完整的圆共有13个,…,若这样铺成一个10×10的正方形图案,则其中完整的圆共有( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com