
分析 根据一次函数的性质,1-2k>0时,y随x的增大而增大,解得k<$\frac{1}{2}$,则2k-1<0,然后根据一次函数图象与系数的关系判断图象经过的象限.
解答 解:∵1-2k>0时,y随x的增大而增大,
∴k<$\frac{1}{2}$,
∵2k-1<0,
∴一次函数图象经过第一、三、四象限.
故答案为<$\frac{1}{2}$,一、三、四.
点评 本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 完成下面的证明.
完成下面的证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
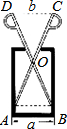 如图,质地均匀的空心圆柱形零件的外直径为a,现用一个交叉钳(AC和BD的长相等)测量,如果$\frac{OA}{OC}=\frac{OB}{OD}=n$,而且CD=b,那么这个零件的厚度为$\frac{a-bn}{2}$.
如图,质地均匀的空心圆柱形零件的外直径为a,现用一个交叉钳(AC和BD的长相等)测量,如果$\frac{OA}{OC}=\frac{OB}{OD}=n$,而且CD=b,那么这个零件的厚度为$\frac{a-bn}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校在一次投掷铅球时,刚出手时铅球离地面$\frac{5}{3}$m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图所示:
某学校在一次投掷铅球时,刚出手时铅球离地面$\frac{5}{3}$m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com