
| A. | 45° | B. | 135° | ||
| C. | 45°或135° | D. | 由两个锐角的大小决定 |
分析 如图,∠ACB=90°,OA、OB分别平分∠BAC和∠ABC,利用角平分线的定义得到∠OAB=$\frac{1}{2}∠$BAC,∠OBA=$\frac{1}{2}$∠ABC,则∠OAB+∠OBA=$\frac{1}{2}$(∠BAC+∠ABC),再根据三角形内角和得到∠BAC+∠ABC=90°,则∠OAB+∠OBA=45°,所以∠AOB=135°,然后利用两直线的夹角为锐角可判定直角三角形的两个锐角平分线的夹角是45°.
解答 解: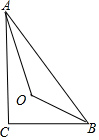 如图,∠ACB=90°,OA、OB分别平分∠BAC和∠ABC,
如图,∠ACB=90°,OA、OB分别平分∠BAC和∠ABC,
∵OA、OB分别平分∠BAC和∠ABC,
∴∠OAB=$\frac{1}{2}∠$BAC,∠OBA=$\frac{1}{2}$∠ABC,
∴∠OAB+∠OBA=$\frac{1}{2}$(∠BAC+∠ABC),
∵∠C=90°,
∴∠BAC+∠ABC=90°,
∴∠OAB+∠OBA=45°,
∴∠AOB=180°-45°=135°,
∴直角三角形的两个锐角平分线的夹角是135°.
故选B.
点评 本题考查了直角三角形的性质:直角三角形两直角边的平方和等于斜边的平方(勾股定理);在直角三角形中,两个锐角互余.直角三角形中,斜边上的中线等于斜边的一半.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
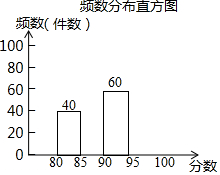 某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:
某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:| 分数段 | 频数 | 百分比 |
| 80≤x<85 | 40 | 20% |
| 85≤x<90 | 80 | 40% |
| 90≤x<95 | 60 | 30% |
| 95≤x<100 | 20 | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
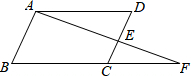 如图,已知:∠DAF=∠F,∠B=∠D,试说明AB∥DC.下面是解答过程,请你在括号内填写理由.
如图,已知:∠DAF=∠F,∠B=∠D,试说明AB∥DC.下面是解答过程,请你在括号内填写理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
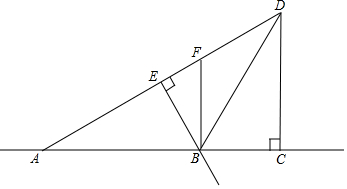 如图所示,DB是∠ADC的平分线,AC⊥CD,∠BED=90°,BF∥CD,∠ADB=30°.
如图所示,DB是∠ADC的平分线,AC⊥CD,∠BED=90°,BF∥CD,∠ADB=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com