
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() ЗжБ№НЛ
ЗжБ№НЛ![]() жсЁЂ
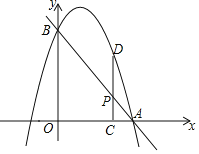
жсЁЂ![]() жсгкЕуAЁЂBЃЌХзЮяЯпЙ§AЃЌBСНЕуЃЌЕуPЪЧЯпЖЮABЩЯвЛЖЏЕуЃЌЙ§ЕуPзїPC
жсгкЕуAЁЂBЃЌХзЮяЯпЙ§AЃЌBСНЕуЃЌЕуPЪЧЯпЖЮABЩЯвЛЖЏЕуЃЌЙ§ЕуPзїPC![]()
![]() жсгкЕуCЃЌНЛХзЮяЯпгкЕуDЃЎ
жсгкЕуCЃЌНЛХзЮяЯпгкЕуDЃЎ
ЃЈ1ЃЉШєХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌЩшЦфЖЅЕуЮЊMЃЌЦфЖдГЦжсНЛABгкЕуNЃЎ
ЃЌЩшЦфЖЅЕуЮЊMЃЌЦфЖдГЦжсНЛABгкЕуNЃЎ
ЂйЧѓЕуMЁЂNЕФзјБъЃЛ
ЂкЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮMNPDЮЊСтаЮЃПВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЕБЕуPЕФКсзјБъЮЊ1ЪБЃЌЪЧЗёДцдкетбљЕФХзЮяЯпЃЌЪЙЕУвдBЁЂPЁЂDЮЊЖЅЕуЕФШ§НЧаЮгы![]() AOBЯрЫЦЃПШєДцдкЃЌЧѓГіТњзуЬѕМўЕФХзЮяЯпЕФНтЮіЪНЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
AOBЯрЫЦЃПШєДцдкЃЌЧѓГіТњзуЬѕМўЕФХзЮяЯпЕФНтЮіЪНЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]()
![]() ЂкД№АИМћНтЮі ЃЈ2ЃЉДцдкЃЌ
ЂкД№АИМћНтЮі ЃЈ2ЃЉДцдкЃЌ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЂйШчЭМ1ЃЌАбХзЮяЯпНтЮіЪНХфГЩЖЅЕуЪНПЩЕУЕНЖЅЕуЮЊ![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌШЛКѓМЦЫуздБфСПЮЊ
ЃЌШЛКѓМЦЫуздБфСПЮЊ![]() ЖдгІЕФвЛДЮКЏЪ§жЕПЩЕУЕН
ЖдгІЕФвЛДЮКЏЪ§жЕПЩЕУЕН![]() ЕузјБъЃЛ
ЕузјБъЃЛ
ЂквзЕУ![]() ЃЌЩш
ЃЌЩш![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌдђ
ЃЌдђ![]() ЃЌгЩгк
ЃЌгЩгк![]() ЃЌИљОнЦНааЫФБпаЮЕФХаЖЈЗНЗЈЃЌЕБ
ЃЌИљОнЦНааЫФБпаЮЕФХаЖЈЗНЗЈЃЌЕБ![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЌМД
ЮЊЦНааЫФБпаЮЃЌМД![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЕУЕНДЫЪБ
ЕУЕНДЫЪБ![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌНгзХМЦЫуГі
ЃЌНгзХМЦЫуГі![]() ЃЌШЛКѓБШНЯ
ЃЌШЛКѓБШНЯ![]() гы
гы![]() ЕФДѓаЁЙиЯЕПЩХаЖЯЦНааЫФБпаЮ
ЕФДѓаЁЙиЯЕПЩХаЖЯЦНааЫФБпаЮ![]() ЪЧЗёЮЊСтаЮЃЛ
ЪЧЗёЮЊСтаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌРћгУЙДЙЩЖЈРэМЦЫуГі![]() ЃЌдйБэЪОГі
ЃЌдйБэЪОГі![]() ЃЌдђПЩМЦЫуГі
ЃЌдђПЩМЦЫуГі![]() ЃЌНгзХБэЪОГіХзЮяЯпНтЮіЪНЮЊ
ЃЌНгзХБэЪОГіХзЮяЯпНтЮіЪНЮЊ![]() ЃЌдђПЩгУ
ЃЌдђПЩгУ![]() БэЪОГіЕу
БэЪОГіЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌгЩгк
ЃЌгЩгк![]() ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЗНЗЈЃЌЕБ
ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЗНЗЈЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌШЛКѓРћгУБШР§аджЪЗжБ№ЧѓГі
ЃЌШЛКѓРћгУБШР§аджЪЗжБ№ЧѓГі![]() ЕФжЕЃЌДгЖјЕУЕНЖдгІЕФХзЮяЯпЕФНтЮіЪНЃЎ
ЕФжЕЃЌДгЖјЕУЕНЖдгІЕФХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ1ЃЉЂйШчЭМ1ЃЌ
![]() ЃЌ
ЃЌ
![]() ЖЅЕуЮЊ
ЖЅЕуЮЊ![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌдђЕу
ЃЌдђЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЂкВЛДцдкЃЎ
РэгЩШчЯТЃК
![]() ЃЌ
ЃЌ
Щш![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЌМД
ЮЊЦНааЫФБпаЮЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЦНааЫФБпаЮ
ЦНааЫФБпаЮ![]() ВЛЮЊСтаЮЃЌ
ВЛЮЊСтаЮЃЌ
![]() ВЛДцдкЕу
ВЛДцдкЕу![]() ЃЌЪЙЫФБпаЮ
ЃЌЪЙЫФБпаЮ![]() ЮЊСтаЮЃЛ
ЮЊСтаЮЃЛ
ЃЈ2ЃЉДцдкЃЎ
ШчЭМ2ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЩшХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
Аб![]() ДњШыЕУ
ДњШыЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
![]() ХзЮяЯпЕФНтЮіЪНЮЊ
ХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЕБ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌДЫЪБХзЮяЯпНтЮіЪНЮЊ
ЃЌДЫЪБХзЮяЯпНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌДЫЪБХзЮяЯпНтЮіЪНЮЊ
ЃЌДЫЪБХзЮяЯпНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФХзЮяЯпЕФНтЮіЪНЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгыxжсЕФЯрНЛЧщПіЃЌЙигкЯТСаНсТлЃК
ЂйЗНГЬax2+bxЃН0ЕФСНИіИљЮЊx1ЃН0ЃЌx2ЃНЉ4ЃЛЂкbЉ4aЃН0ЃЛЂл9a+3b+cЃМ0ЃЛЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ
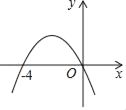
A. 0ИіB. 1ИіC. 2ИіD. 3Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
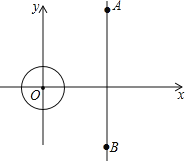
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌ![]() ЕФАыОЖЮЊ1ЃЌAЁЂBСНЕузјБъЗжБ№ЮЊ
ЕФАыОЖЮЊ1ЃЌAЁЂBСНЕузјБъЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() вбжЊЕуPЪЧ
вбжЊЕуPЪЧ![]() ЩЯЕФвЛЕуЃЌЕуQЪЧЯпЖЮABЩЯЕФвЛЕуЃЌЩш
ЩЯЕФвЛЕуЃЌЕуQЪЧЯпЖЮABЩЯЕФвЛЕуЃЌЩш![]() ЕФУцЛ§ЮЊSЃЌЕБ
ЕФУцЛ§ЮЊSЃЌЕБ![]() ЮЊжБНЧШ§НЧаЮЪБЃЌSЕФШЁжЕЗЖЮЇЮЊ______ЃЎ
ЮЊжБНЧШ§НЧаЮЪБЃЌSЕФШЁжЕЗЖЮЇЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЮЊИпЯпЃЌЕу
ЮЊИпЯпЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌгыБп
ЃЌгыБп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБ![]() ЪБЃЌЧѓжЄЃК
ЪБЃЌЧѓжЄЃК![]()
ЃЈ2ЃЉШчЭМ2ЃЌЕБ![]() ЪБЃЌдђЯпЖЮ
ЪБЃЌдђЯпЖЮ![]() ЁЂ
ЁЂ![]() ЕФЪ§СПЙиЯЕЮЊ ЃЛ
ЕФЪ§СПЙиЯЕЮЊ ЃЛ
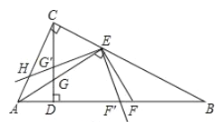
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЃЌа§зЊКѓ
ЃЌа§зЊКѓ![]() БпЫљдкЕФжБЯпгыБп
БпЫљдкЕФжБЯпгыБп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌ
ЃЌ![]() БпЫљдкЕФжБЯпгыБп
БпЫљдкЕФжБЯпгыБп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌгыИпЯп
ЃЌгыИпЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() HЕФГЄЃЎ
HЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
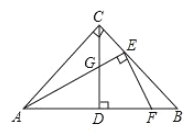
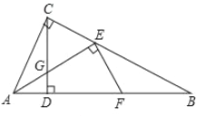
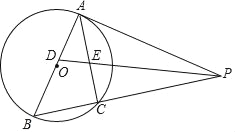
ЁОЬтФПЁПШчЭМЃЌвдABЮЊжБОЖЕФЁбOЭтНггкЁїABCЃЌЙ§AЕуЕФЧаЯпAPгыBCЕФбгГЄЯпНЛгкЕуPЃЌЁЯAPBЕФЦНЗжЯпЗжБ№НЛABЃЌACгкЕуDЃЌEЃЌЦфжаAEЃЌBDЃЈAEЃМBDЃЉЕФГЄЪЧвЛдЊЖўДЮЗНГЬx2Љ5x+6=0ЕФСНИіЪЕЪ§ИљЃЎ
ЃЈ1ЃЉЧѓжЄЃКPABD=PBAEЃЛ
ЃЈ2ЃЉдкЯпЖЮBCЩЯЪЧЗёДцдквЛЕуMЃЌЪЙЕУЫФБпаЮADMEЪЧСтаЮЃПШєДцдкЃЌЧыИјгшжЄУїЃЌВЂЧѓЦфУцЛ§ЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬт6ЗжЃЉМзЁЂввСНШЫНјааУўХЦгЮЯЗЃЎЯжгаШ§еХаЮзДДѓаЁЭъШЋЯрЭЌЕФХЦЃЌе§УцЗжБ№БъгаЪ§зж2ЃЌ3ЃЌ5ЃЎНЋШ§еХХЦБГУцГЏЩЯЃЌЯДдШКѓЗХдкзРзгЩЯЃЎ
ЃЈ1ЃЉМзДгжаЫцЛњГщШЁвЛеХХЦЃЌМЧТМЪ§зжКѓЗХЛиЯДдШЃЌввдйЫцЛњГщШЁвЛеХЃЎЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓСНШЫГщШЁЯрЭЌЪ§зжЕФИХТЪЃЛ
ЃЈ2ЃЉШєСНШЫГщШЁЕФЪ§зжКЭЮЊ2ЕФБЖЪ§ЃЌдђМзЛёЪЄЃЛШєГщШЁЕФЪ§зжКЭЮЊ5ЕФБЖЪ§ЃЌдђввЛёЪЄЃЎетИігЮЯЗЙЋЦНТ№ЃПЧыгУИХТЪЕФжЊЪЖМгвдНтЪЭЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцФкгЩМЋЕуЁЂМЋжсКЭМЋОЖзщГЩЕФзјБъЯЕНазіМЋзјБъЯЕЃЎШчЭМЃЌдкЦНУцЩЯШЁЖЈвЛЕуOГЦЮЊМЋЕуЃЛДгЕуOГіЗЂв§вЛЬѕЩфЯпOxГЦЮЊМЋжсЃЛЯпЖЮOPЕФГЄЖШГЦЮЊМЋОЖЃЎЕуPЕФМЋзјБъОЭПЩвдгУЯпЖЮOPЕФГЄЖШвдМАДгOxзЊЖЏЕНOPЕФНЧЖШЃЈЙцЖЈФцЪБеыЗНЯђзЊЖЏНЧЖШЮЊе§ЃЉРДШЗЖЈЃЌМДPЃЈ3ЃЌ60ЁуЃЉЛђPЃЈ3ЃЌЉ300ЁуЃЉЛђPЃЈ3ЃЌ420ЁуЃЉЕШЃЌдђЕуPЙигкЕуOГЩжааФЖдГЦЕФЕуQЕФМЋзјБъБэЪОВЛе§ШЗЕФЪЧЃЈ ЃЉ
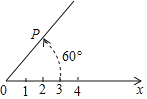
A. QЃЈ3ЃЌ240ЁуЃЉ B. QЃЈ3ЃЌЉ120ЁуЃЉ C. QЃЈ3ЃЌ600ЁуЃЉ D. QЃЈ3ЃЌЉ500ЁуЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаСНдђВФСЯЃЌЛиД№ЮЪЬтЃЌ
ВФСЯвЛЃКЖЈвхжБЯпyЃНax+bгыжБЯпyЃНbx+aЛЅЮЊЁАЛЅжњжБЯпЁБЃЌР§ШчЃЌжБЯпyЃНx+4гыжБyЃН4x+1ЛЅЮЊЁАЛЅжњжБЯпЁА
ВФСЯЖўЃКЖдгкЦНУцжБНЧзјБъЯЕжаЕФШЮвтСНЕуP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЃЌP1ЁЂP2СНЕуМфЕФжБНЧОрРыdЃЈP1ЃЌP2ЃЉЃН|x1Љx2|+|y1Љy2|ЃЎР§ШчЃКQ1ЃЈЉ3ЃЌ1ЃЉЁЂQ2ЃЈ2ЃЌ4ЃЉСНЕуМфЕФжБНЧОрРыЮЊdЃЈQ1ЃЌQ2ЃЉЃН|Љ3Љ2|+|1Љ4|ЃН8
ЩшP0ЃЈx0ЃЌy0ЃЉЮЊвЛИіЖЈЕуЃЌQЃЈxЃЌyЃЉЪЧжБЯпyЃНax+bЩЯЕФЖЏЕуЃЌЮвУЧАбdЃЈP0ЃЌQЃЉЕФзюаЁжЕНазіP0ЕНжБЯпyЃНax+bЕФжБНЧОрРыЃЎ
ЃЈ1ЃЉМЦЫуSЃЈЉ1ЃЌ6ЃЉЃЌTЃЈЉ2ЃЌ3ЃЉСНЕуМфЕФжБНЧОрРыdЃЈSЃЌTЃЉЃНЁЁ ЁЁЃЌжБЯпyЃН2x+3ЩЯЕФвЛЕуHЃЈaЃЌbЃЉгжЪЧЫќЕФЁАЛЅжњжБЯпЁБЩЯЕФЕуЃЌЧѓЕуHЕФзјБъЃЎ
ЃЈ2ЃЉЖдгкжБЯпyЃНax+bЩЯЕФШЮвтвЛЕуMЃЈmЃЌnЃЉЃЌЖМгаЕуNЃЈ3mЃЌ2mЉ3nЃЉдкЫќЕФЁАЛЅжњжБЯпЁБЩЯЃЌЪдЧѓЕуLЃЈ5ЃЌЉ![]() ЃЉЕНжБЯпyЃНax+bЕФжБНЧОрРыЃЎ
ЃЉЕНжБЯпyЃНax+bЕФжБНЧОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаетбљвЛИіЬтФПЃК
АДееИјЖЈЕФМЦЫуГЬађЃЌШЗЖЈЪЙДњЪ§ЪНnЃЈn+2ЃЉДѓгк2000ЕФnЕФзюаЁе§ећЪ§жЕЃЎЯывЛЯыЃЌдѕбљбИЫйевЕНетИіnжЕЃЌЧыгыЭЌбЇУЧНЛСїФуЕФЬхЛсЃЎ
аЁССГЂЪдМЦЫуСЫМИзщnКЭnЃЈn+2ЃЉЕФЖдгІжЕШчЯТБэЃК
n | 50 | 40 | |
nЃЈn+2ЃЉ | 2600 | 1680 |
ЃЈ1ЃЉЧыФуМЬајаЁССЕФГЂЪдЃЌдйЫуМИзщЬюдкЩЯБэжаЃЈМИзщЫцвтЃЌздМКЛИёЃЉЃЌВЂаДГіТњзуЬтФПвЊЧѓЕФnЕФжЕЃЛ
ЃЈ2ЃЉНсКЯЩЯЪіЙ§ГЬЃЌЖдгкЁАдѕбљбИЫйевЕНnжЕЁБетИіЮЪЬтЃЌЫЕЫЕФуЕФЯыЗЈЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com