
【题目】如图,AE是半圆O的直径,弦AB=BC=2 ![]() ,弦CD=DE=2,连结OB,OD,求图中两个阴影部分的面积和.
,弦CD=DE=2,连结OB,OD,求图中两个阴影部分的面积和. 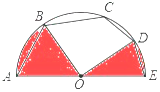
【答案】解:∵弦AB=BC,弦CD=DE, ∴点B是弧AC的中点,点D是弧CE的中点,
∴∠BOD=90°,
过点O作OF⊥BC于点F,OG⊥CD于点G.
则BF=FC= ![]() ,CG=GD=1,∠FOG=45°,
,CG=GD=1,∠FOG=45°,
在四边形OFCG中,∠FCD=135°,
过点C作CN∥OF,交OG于点N,
则∠FCN=90°,∠NCG=135°﹣90°=45°,
∴△CNG为等腰三角形,
∴CG=NG=1,
过点N作NM⊥OF于点M,则MN=FC= ![]() ,
,
在等腰三角形MNO中,NO= ![]() MN=2,
MN=2,
∴OG=ON+NG=3,
在Rt△OGD中,OD= ![]() =
= ![]() =
= ![]() ,
,
即圆O的半径为 ![]() ,
,
故S阴影=S扇形OBD= 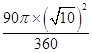 =
= ![]() π.
π.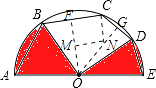
【解析】根据弦AB=BC,弦CD=DE,可得∠BOD=90°,∠BOD=90°,过点O作OF⊥BC于点F,OG⊥CD于点G,在四边形OFCG中可得∠FCD=135°,过点C作CN∥OF,交OG于点N,判断△CNG、△OMN为等腰直角三角形,分别求出NG、ON,继而得出OG,在Rt△OGD中求出OD,即得圆O的半径,代入扇形面积公式求解即可.
【考点精析】本题主要考查了扇形面积计算公式的相关知识点,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】定义:我们把对角线相等的四边形叫做和美四边形.
![]() 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子.
![]() 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
![]() 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,![]() ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为![]() BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
![]()
A. 点E B. 点F C. 点M D. 点N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
(2)如图2,∠BOE=2∠AOE,OF平分∠AOB,∠EOF=20°.求∠AOB.
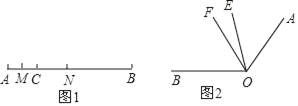
查看答案和解析>>
科目:初中数学 来源: 题型:
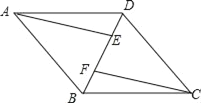
【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“城市发展,交通先行”,我市启动了缓堵保畅的高架桥快速通道建设工程,建成后将大大提升道路的通行能力.研究表明,某种情况下,高架桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,且当0<x≤28时,V=80;当28<x≤188时,V是x的一次函数.函数关系如图所示.
(1)求当28<x≤188时,V关于x的函数表达式;
(2)请你直接写出车流量P和车流密度x之间的函数表达式;当x为多少时,车流量P(单位:辆/时)达到最大,最大值是多少?
(注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() 的图象位于第二、第四象限,那么关于x的一元二次方程x2+2x+k=0的根的情况是( )
的图象位于第二、第四象限,那么关于x的一元二次方程x2+2x+k=0的根的情况是( )
A.方程有两个不想等的实数根
B.方程不一定有实数根
C.方程有两个相等的实数根
D.方程没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,每年的4月23日被联合国教科文组织确定为“世界读书日”某校本学年开展了读书活动,在这次活动中,八年级![]() 班40名学生读书册数的情况如表
班40名学生读书册数的情况如表
读书册数 | 4 | 5 | 6 | 7 | 8 |
人数 | 6 | 4 | 10 | 12 | 8 |
根据表中的数据,求:
(1)该班学生读书册数的平均数;
(2)该班学生读书册数的中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的长为2 ![]() cm,对角线交于点O,以AB,AO为邻边做平行四边形AOCB,对角线交于点O,以AB、AO1为邻边做平行四边形AO1C1B,…,依此类推,则平行四边形AO6C6B的面积为cm2 .
cm,对角线交于点O,以AB,AO为邻边做平行四边形AOCB,对角线交于点O,以AB、AO1为邻边做平行四边形AO1C1B,…,依此类推,则平行四边形AO6C6B的面积为cm2 . 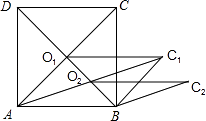
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com