
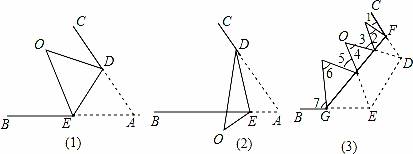
(1)如图(1),把三角形纸片ABC的角A沿DE折起(DE为折痕),使顶点A在∠A的内部,点A的对称点为点O,判断∠O、∠ODC、∠BEO的大小关系,并写出证明过程.
(2)如图(2),把三角形纸片ABC的角A沿DE折起(DE为折痕),使顶点A在∠A的外部,点A的对称点为点O,判断∠O、∠ODC、∠BEO的大小关系吗?(只写出答案,无需证明).
(3)在图(1)的基础上再以FG为折痕叠纸片,形成如图(3)的形状.判断∠1、∠2、∠3、∠4、∠5、∠6、∠7的之间大小关系吗?(只写出答案,无需证明).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
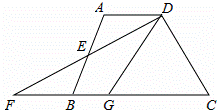
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
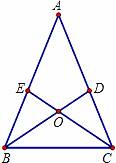
如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE;上述结论一定正确的是( )
|
| A. | ①②③ | B. | ②③④ | C. | ①③⑤ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com