
科目:初中数学 来源: 题型:选择题
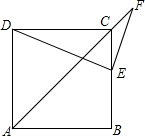 如图,正方形ABCD的边长为10+5$\sqrt{2}$,点E在边CB上,点F在AC的延长线上,EF⊥DE.若CE=CF,则CE的值为( )
如图,正方形ABCD的边长为10+5$\sqrt{2}$,点E在边CB上,点F在AC的延长线上,EF⊥DE.若CE=CF,则CE的值为( )| A. | 5 | B. | 5$\sqrt{2}$ | C. | 10 | D. | 10$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
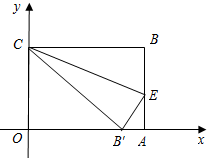 已知如图,在直角坐标系中放入一个边长OA为8的长方形纸片ABCO.
已知如图,在直角坐标系中放入一个边长OA为8的长方形纸片ABCO.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.5×108 | B. | 25×106 | C. | 0.25×108 | D. | 2.5×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 检测某批灯泡的使用寿命,采用普查的方式 | |
| B. | “嫦娥三号”发射前,对重要零部件的检查,采用抽样调查的方式 | |
| C. | 为了了解全班学生的身体状况,采用普查的方式 | |
| D. | 了解泾阳电视台“新闻播报”栏目的收视率情况,采用普查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
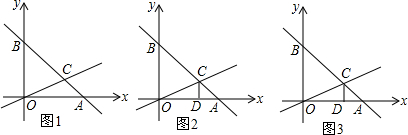
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com