
【题目】对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
(尝试)
(1)当t=2时,抛物线y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的顶点坐标为 ;
(2)判断点A是否在抛物线L上;
(3)求n的值;
(发现)
通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为 .
(应用)
二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.

【答案】[尝试](1)(1,﹣2);(2)点A在抛物线L上;(3)n=6;[发现](2,0),(﹣1,6);[应用]不是,理由见解析.
【解析】
[尝试]
(1)将t的值代入“再生二次函数”中,通过配方可得到顶点的坐标;
(2)将点A的坐标代入抛物线L直接进行验证即可;
(3)已知点B在抛物线L上,将该点坐标代入抛物线L的解析式中直接求解,即可得到n的值.
[发现]
将抛物线L展开,然后将含t值的式子整合到一起,令该式子为0(此时无论t取何值都不会对函数值产生影响),即可求出这个定点的坐标.
[应用]
将[发现]中得到的两个定点坐标代入二次函数y=-3x2+5x+2中进行验证即可.
解:[尝试]
(1)∵将t=2代入抛物线L中,得:
y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)=2x2﹣4x=2(x﹣1)2﹣2,
∴此时抛物线的顶点坐标为:(1,﹣2).
(2)∵将x=2代入y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4),得 y=0,
∴点A(2,0)在抛物线L上.
(3)将x=﹣1代入抛物线L的解析式中,得:
n=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)=6.
[发现]
∵将抛物线L的解析式展开,得:
y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)=t(x﹣2)(x+1)﹣2x+4
当x=2时,y=0,当x=-1时,y=6,与t无关,
∴抛物线L必过定点(2,0)、(﹣1,6).
[应用]
将x=2代入y=﹣3x2+5x+2,y=0,即点A在抛物线上.
将x=﹣1代入y=﹣3x2+5x+2,计算得:y=﹣6≠6,
即可得抛物线y=﹣3x2+5x+2不经过点B,
∴二次函数y=﹣3x2+5x+2不是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”.


科目:初中数学 来源: 题型:
【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如下表格:
的图象可以得到如下表格:
|
|
|
|
|
|
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可得到如下表格:
的图象可得到如下表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() 的图象;
的图象;

观察函数![]() 的图象,
的图象,
补全下面的表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法,解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
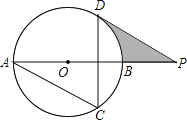
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于6cm2?
(2)在(1)中,△PQB的面积能否等于8cm2?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化课改,落实立德树人目标,某学校设置了以下四门拓展性课程:A.数学思维,B.文学鉴赏,C.红船课程,D.3D打印,规定每位学生选报一门.为了解学生的报名情况,随机抽取了部分学生进行调查,并制作成如下两幅不完整的统计图,请回答下列问题:
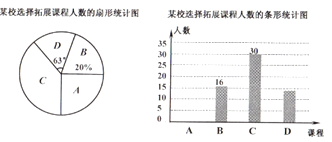
(1)求这次被调查的学生人数;
(2)请将条形统计图补充完整;
(3)假如全校有学生1000人,请估计选报“红船课程”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 如图所示,点
如图所示,点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离均等于
三点的距离均等于![]() (
(![]() 为常数),到点
为常数),到点![]() 的距离等于
的距离等于![]() 的所有点组成图形
的所有点组成图形![]() . 射线
. 射线![]() 与射线
与射线![]() 关于
关于![]() 对称,过点 C作
对称,过点 C作![]() 于
于![]() .
.
(1)依题意补全图形(保留作图痕迹);
(2)判断直线![]() 与图形
与图形![]() 的公共点个数并加以证明.
的公共点个数并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上。甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地。两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示。
(分钟)之间的函数关系如图所示。
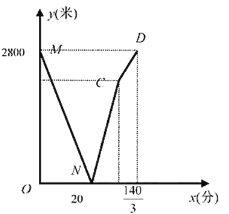
(1)当![]() ____________分钟时甲、乙两人相遇,乙的速度为__________米/分钟,点
____________分钟时甲、乙两人相遇,乙的速度为__________米/分钟,点![]() 的坐标为_____________;
的坐标为_____________;
(2)求出甲、乙两人相遇后![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当乙到达距学校800米处时,求甲、乙两人之间的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:
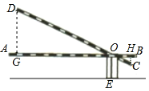
【题目】如图,某小区门口的栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为3.5米,OA的长为3米,点C到AB的距离为0.3米,支柱OE的高为0.6米,那么栏杆端点D离地面的距离为____________米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了配合全市“创建全国文明城市”活动,某校共1200名学生参加了学校组织的创建全国文明城市知识竞赛,拟评出四名一等奖.
(1)求每一位同学获得一等奖的概率;
(2)学校对本次竞赛获奖情况进行了统计,其中七、八年级分别有一名同学获得一等奖,九年级有2名同学获得一等奖,现从获得一等奖的同学中任选两人参加全市决赛,请通过列表或画树状图的方法,求所选出的两人中既有七年级又有九年级同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com