
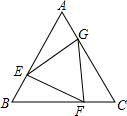
 如图,已知正△ABC的边长为2,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
如图,已知正△ABC的边长为2,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )| A. |  | B. |  | C. |  | D. | 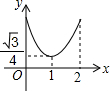 |
分析 根据题意,易得△AEG、△BEF、△CFG三个三角形全等,且在△AEG中,AE=x,AG=2-x;可得△AEG的面积y与x的关系;进而可判断出y关于x的函数的图象的大致形状.
解答 解:根据题意,有AE=BF=CG,且正三角形ABC的边长为2,
故BE=CF=AG=2-x;
故△AEG、△BEF、△CFG三个三角形全等.
在△AEG中,AE=x,AG=2-x.
则S△AEG=$\frac{1}{2}$AE×AG×sinA=$\frac{\sqrt{3}}{4}$x(2-x);
故y=S△ABC-3S△AEG
=$\sqrt{3}$-3×$\frac{\sqrt{3}}{4}$x(2-x)=$\frac{\sqrt{3}}{4}$(3x2-6x+4).
故可得其大致图象应类似于抛物线,且抛物线开口方向向上;
故选:D.
点评 本题考查动点问题的函数图象问题,用图象解决问题时,要理清图象的含义即会识图.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:填空题
 如图,直角梯形ABCD是一机器零件的横断面,已知DC=20cm,BC=40cm,∠DCB=30°,求AD的长为40-10$\sqrt{3}$cm.
如图,直角梯形ABCD是一机器零件的横断面,已知DC=20cm,BC=40cm,∠DCB=30°,求AD的长为40-10$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
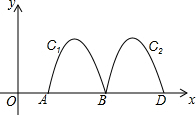 如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )| A. | -2<m<$\frac{1}{8}$ | B. | -3<m<-$\frac{7}{4}$ | C. | -3<m<-2 | D. | -3<m<-$\frac{15}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )| A. | AF=AE | B. | △ABE≌△AGF | C. | EF=2$\sqrt{5}$ | D. | AF=EF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )| A. |  | B. |  | C. | 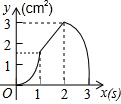 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com