
分析 (1)根据阅读知识找到规律即可求解;
(2)原式变形为-$\frac{1}{3}$(-2-1)×[(-2)2014+(-2)2013+(-2)2012+(-2)2011+(-2)2010…+(-2)3+(-2)2+(-2)+1],计算即可得到结果.
解答 解:(1)(x-1)×(xn+xn-1+…+x+1)=xn+1-1(n为正整数);
(2)22014-22013+22012-22011+22010…-23+22-2+1
=-$\frac{1}{3}$×(-2-1)×[(-2)2014+(-2)2013+(-2)2012+(-2)2011+(-2)2010…+(-2)3+(-2)2+(-2)+1]
=-$\frac{1}{3}$×[(-2)2015-1]
=$\frac{{2}^{2015}+1}{3}$.
故答案为:xn+1-1;$\frac{{2}^{2015}+1}{3}$.
点评 此题考查了平方差公式,弄清题中的规律是解本题的关键.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
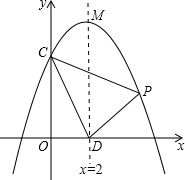 如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,
如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 型号 | A | B |
| 单个盒子容量(升) | 2 | 3 |
| 单价(元) | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com