
”¾ĢāÄæ”æČēĶ¼1£¬µćDĪŖ”÷ABC±ßBCµÄŃÓ³¤ĻßÉĻŅ»µć£®
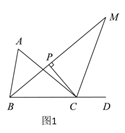
£Ø1£©Čō”ĻA”Ć”ĻABC=3”Ć4£¬”ĻACD=140”ć£¬Ēó”ĻAµÄ¶ČŹż£»
£Ø2£©Čō”ĻABCµÄ½ĒĘ½·ÖĻßÓė”ĻACDµÄ½ĒĘ½·ÖĻß½»ÓŚµćM£¬¹żµćC×÷CP”ĶBMÓŚµćP£®
ĒóÖ¤£ŗ ![]() £»
£»
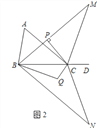
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬½«”÷MBCŅŌÖ±ĻßBCĪŖ¶Ō³ĘÖį·ÕŪµĆµ½”÷NBC£¬”ĻNBCµÄ½ĒĘ½·ÖĻßÓė”ĻNCBµÄ½ĒĘ½·ÖĻß½»ÓŚµćQ£ØČēĶ¼2£©£¬ŹŌĢ½¾æ”ĻBQCÓė”ĻAÓŠŌõŃłµÄŹżĮæ¹ŲĻµ£¬ĒėŠ“³öÄćµÄ²ĀĻė²¢Ö¤Ć÷£®
”¾“š°ø”æ£Ø1£©60”ć”ć£»
£Ø2£©Ö¤Ć÷¼ū½āĪö£»
£Ø3£©”ĻBQC=90”ć+![]() ”ĻA£¬ĄķÓɼū½āĪö.
”ĻA£¬ĄķÓɼū½āĪö.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ĻČøł¾Ż”ĻA£ŗ”ĻABC=3£ŗ4£¬Éč”ĻA=3k£¬”ĻABC=4k£¬ŌŁÓÉČż½ĒŠĪĶā½ĒµÄŠŌÖŹĒó³ökµÄÖµ£¬½ų¶ųæÉµĆ³ö½įĀŪ£»
£Ø2£©øł¾ŻČż½ĒŠĪĶā½ĒµÄŠŌÖŹµĆ³ö”ĻM=”ĻMCD-”ĻMBC£¬”ĻA=”ĻACD-”ĻABC£®ŌŁÓÉMC”¢MB·Ö±šĘ½·Ö”ĻACD”¢”ĻABCµĆ³ö![]() ,
, ![]() ,
,
¹Ź![]() ,øł¾ŻCP”ĶBM¼“æÉµĆ³ö½įĀŪ£»
,øł¾ŻCP”ĶBM¼“æÉµĆ³ö½įĀŪ£»
£Ø3£©øł¾ŻBQĘ½·Ö”ĻCBN£¬CQĘ½·Ö”ĻBCNæÉÖŖ![]() ,
, ![]() £¬ŌŁøł¾ŻČż½ĒŠĪÄŚ½ĒŗĶ¶ØĄķæÉÖŖ£¬
£¬ŌŁøł¾ŻČż½ĒŠĪÄŚ½ĒŗĶ¶ØĄķæÉÖŖ£¬ ![]() ,øł¾ŻÖį¶Ō³ĘŠŌÖŹÖŖ£ŗ
,øł¾ŻÖį¶Ō³ĘŠŌÖŹÖŖ£ŗ
”ĻM=”ĻN£¬ÓÉ“ĖæÉµĆ³ö½įĀŪ£®
£Ø1£©½ā£ŗ”ß![]() £¬”ąæÉÉč
£¬”ąæÉÉč![]() £®
£®
ÓÖ”ß![]()
![]() ”ć£¬
”ć£¬
”ą![]() ”ć£¬
”ć£¬
½āµĆ ![]() ”ć£®
”ć£®
”ą![]() ”ć£®
”ć£®
£Ø2£©Ö¤Ć÷£ŗ
![]()
£Ø3£©²ĀĻė”ĻBQC=90”ć+![]() ”ĻA£®
”ĻA£®
Ö¤Ć÷ČēĻĀ£ŗ ”ßBQĘ½·Ö”ĻCBN£¬CQĘ½·Ö”ĻBCN£¬
”ą![]() £¬
£¬
”ą![]()
![]()
![]() £®
£®
ÓÉ£Ø2£©ÖŖ£ŗ ![]() £¬ÓÖÓÉÖį¶Ō³ĘŠŌÖŹÖŖ£ŗ”ĻM=”ĻN£¬
£¬ÓÖÓÉÖį¶Ō³ĘŠŌÖŹÖŖ£ŗ”ĻM=”ĻN£¬
”ą![]() £®
£®
±¾Ģāæ¼²éĮĖČż½ĒŠĪµÄÄŚ½ĒŗĶ£¬Čż½ĒŠĪĶā½ĒµÄŠŌÖŹ£¬ÕŪµžµÄŠŌÖŹ.£Ø1£©¼ū±ČÉč²Ī£¬Č»ŗóøł¾ŻĶā½ĒµÄŠŌÖŹĒó½ā£»£Ø2£©½įŗĻ½ĒĘ½·ÖĻßŗĶĶā½ĒµÄŠŌÖŹĒó½ā£»£Ø2£©øł¾ŻÖį¶Ō³ĘµÄŠŌÖŹŗĶ£Ø2£©µÄ½įĀŪĒó½ā.


 ŌĘÄĻŹ¦“óø½Š”Ņ»ĻßĆūŹ¦ĢįÓÅ×÷ŅµĻµĮŠ“š°ø
ŌĘÄĻŹ¦“óø½Š”Ņ»ĻßĆūŹ¦ĢįÓÅ×÷ŅµĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖĮĖ½āČ«Š£1500Ćūѧɜ¶ŌѧŠ£ÉčÖƵĥŗĒņ”¢ÓšĆ«Ēņ”¢Ę¹ÅŅĒņ”¢Ģßė¦×Ó”¢ĢųÉž¹²5ĻīĢåÓż»ī¶ÆµÄĻ²°®Ēéæö£¬ŌŚČ«Š£·¶Ī§ÄŚĖ껜³é²é²æ·Öѧɜ£¬¶ŌĖūĆĒĻ²°®µÄĢåÓżĻīÄæ£ØĆæČĖֻєŅ»Ļī£©½ųŠŠĮĖĪŹ¾ķµ÷²é£¬½«Ķ³¼ĘŹż¾Ż»ęÖĘ³ÉČēĶ¼Į½·ł²»ĶźÕūĶ³¼ĘĶ¼£¬Ēėøł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠø÷Ģā£®
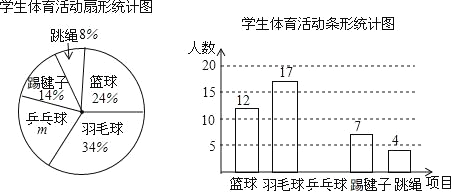
£Ø1£©m= %£¬Õā“Ī¹²³éČ”ĮĖ Ćūѧɜ½ųŠŠµ÷²é£»²¢²¹Č«ĢõŠĪĶ¼£»
£Ø2£©ĒėÄć¹Ą¼ĘøĆŠ£Ō¼ÓŠ ĆūѧɜĻ²°®“ņĄŗĒņ£»
£Ø3£©ĻÖѧŠ£×¼±ø“ÓĻ²»¶ĢųÉž»ī¶ÆµÄ4ČĖ£ØȿĊŅ»Å®£©ÖŠĖ껜єȔ2ČĖ½ųŠŠĢåÄܲāŹŌ£¬ĒėĄūÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·Ø£¬Ēó³éµ½Ņ»ÄŠŅ»Å®Ń§ÉśµÄøÅĀŹŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
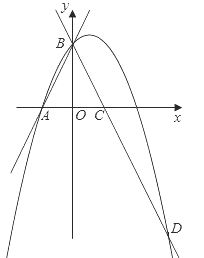
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy=2x+2ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£¬°Ń”÷AOBŃŲyÖį·ÕŪ£¬µćAĀäµ½µćC£¬¹żµćBµÄÅ×ĪļĻßy=-x2+bx+cÓėÖ±ĻßBC½»ÓŚµćD£Ø3£¬-4£©£®
£Ø1£©ĒóÖ±ĻßBDŗĶÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ŌŚµŚŅ»ĻóĻŽÄŚµÄÅ×ĪļĻßÉĻ£¬ŹĒ·ń“ęŌŚŅ»µćM£¬×÷MN“¹Ö±ÓŚxÖį£¬“¹×ćĪŖµćN£¬Ź¹µĆŅŌM”¢O”¢NĪŖ¶„µćµÄČż½ĒŠĪÓė”÷BOCĻąĖĘ£æČō“ęŌŚ£¬Ēó³öµćMµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©ŌŚÖ±ĻßBDÉĻ·½µÄÅ×ĪļĻßÉĻÓŠŅ»¶ÆµćP£¬¹żµćP×÷PH“¹Ö±ÓŚxÖį£¬½»Ö±ĻßBDÓŚµćH£¬µ±ĖıߊĪBOHPŹĒĘ½ŠŠĖıߊĪŹ±£¬ŹŌĒó¶ÆµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ“śŹżŹ½£m2£«4m£4£¬ĪŽĀŪmČ”ČĪŗĪÖµ£¬ĖüµÄÖµŅ»¶ØŹĒ£Ø £©
A. ÕżŹżB. øŗŹżC. ·ĒÕżŹżD. ·ĒøŗŹż
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĆüĢāÖŠµÄÕęĆüĢāŹĒ
A.Čżøö½ĒĻąµČµÄĖıߊĪŹĒ¾ŲŠĪ
B.¶Ō½ĒĻß»„Ļą“¹Ö±ĒŅĻąµČµÄĖıߊĪŹĒÕż·½ŠĪ
C.Ė³“ĪĮ¬½Ó¾ŲŠĪĖıßÖŠµćµĆµ½µÄĖıߊĪŹĒĮāŠĪ
D.ÕżĪå±ßŠĪ¼ČŹĒÖį¶Ō³ĘĶ¼ŠĪÓÖŹĒÖŠŠÄ¶Ō³ĘĶ¼ŠĪ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĀĆŠŠÉē×éĶÅČ„ĶāµŲĀĆÓĪ£¬30ČĖĘš×éĶÅ£¬ĆæČĖµ„¼Ū800ŌŖ£®ĀĆŠŠÉē¶Ō³¬¹ż30ČĖµÄĶÅøųÓčÓÅ»Ż£¬¼“ĀĆŠŠĶŵÄČĖŹżĆæŌö¼ÓŅ»ČĖ£¬ĆæČĖµÄµ„¼Ū¾Ķ½µµĶ10ŌŖ£®µ±Ņ»øöĀĆŠŠĶŵÄČĖŹżŹĒ______ČĖŹ±£¬ÕāøöĀĆŠŠÉēæÉŅŌ»ńµĆ×ī“óµÄÓŖŅµ¶ī£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£Øx+y£©2=1£¬£Øx©y£©2=49£¬Ēóx2+y2ÓėxyµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij³ĒŹŠ°“ŅŌĻĀ¹ę¶ØŹÕČ”ĆæŌĀĆŗĘų·Ń£¬ÓĆĆŗĘų²»³¬¹ż60Į¢·½Ć×£¬°“ĆæĮ¢·½Ć×0.8ŌŖŹÕ·Ń£»Čē¹ū³¬¹ż60Į¢·½Ć×£¬ ³¬¹ż²æ·Ö°“ĆæĮ¢·½Ć×1.2ŌŖŹÕ·Ń.ŅŃÖŖ¼×ÓĆ»§Ä³ŌĀ·ŻÓĆĆŗĘų80ĆæĮ¢·½Ć×£¬ÄĒĆ“ÕāøöŌĀ¼×ÓĆ»§Ó¦½»ĆŗĘų·Ń ( )
A. 64ŌŖ B. 66ŌŖ C. 72ŌŖ D. 96ŌŖ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com