
【题目】如图所示、方格纸中每个小正方的边长都是单位1,△ABC在平面直角坐标系中的位置图所示.
(1)将△ABC向右平移4个单位后得到△A![]() B
B![]() C
C![]() ,请画出△A
,请画出△A![]() B
B![]() C
C![]() ,并直接写出点C
,并直接写出点C![]() 的坐标;
的坐标;
(2)作出△A![]() B
B![]() C
C![]() 关于x轴的对称图形△A
关于x轴的对称图形△A![]() B
B![]() C
C![]() ,并直接写出点A
,并直接写出点A![]() 的坐标;
的坐标;
(3)请由图形直接判断以点C![]() 、C
、C![]() 、B
、B![]() 、B
、B![]() ,为顶点的四边形是什么四边形?并求出它的面积.
,为顶点的四边形是什么四边形?并求出它的面积.
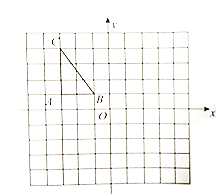
【答案】(1)见解析,C1(1,4);(2)见解析,A2(1,-1);(3)四边形C1C2B2B1是等腰梯形,面积为10.
【解析】
(1)把△ABC的各个顶点向右平移4个单位后顺次连接即可;
(2)得到△A1B1C1的各个顶点关于x轴的对称点,顺次连接,根据A2所在象限及距离坐标轴的距离可得相应坐标;
(3)易得为梯形,根据梯形面积计算即可.
解:(1)将A、B、C分别向右平移4个单位得到A1、B1、C1,再连接A1B1、B1C1、A1C1,则△A1B1C1即为所求,如图所示,由图可知,C1在第一象限距x轴的距离为4,距y轴的距离为1, 则C1(1,4);
(2)分别作出A1、B1、C1关于x轴的对称点A2、B2、C2,再连接A2B2、B2C2、A2C2,则△A2B2C2即为所求,如图所示,由图可知,A2在第四象限且距x轴、y轴的距离均为1,则A2(1,-1);
(3)由作图可知,C1C2∥B1B2,B1C1= B2C2,
∴四边形C1C2B2B1是等腰梯形,
由图可得:B1B2=2,C1C2=8,A1B1=2,
∴梯形的面积=![]() ×(B1B2+C1C2)×A1B1=
×(B1B2+C1C2)×A1B1=![]() ×(2+8)×2=10.
×(2+8)×2=10.



科目:初中数学 来源: 题型:
【题目】某送奶公司计划在三栋楼之间建一个取奶站,三栋楼在同一条直线,顺次为A楼、B楼、C楼,其中A楼与B楼之间的距离为40米,B楼与C楼之间的距离为60米.已知A楼每天有20人取奶,B楼每天有70人取奶,C楼每天有60人取奶,送奶公司提出两种建站方案.
方案一:让每天所有取奶的人到奶站的距离总和最小;
方案二:让每天A楼与C楼所有取奶的人到奶站的距离之和等于B楼所有取奶的人到奶站的距离之和.
(1)若按照方案一建站,取奶站应建在什么位置?
(2)若按照方案二建站,取奶站应建在什么位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象与y=x-1的图象平行,且经过点(2,6).
(1)求一次函数y=kx+b的表达式.
(2)求这个一次函数y=kx+b与坐标轴的两个交点坐标,并在直角坐标系中画出这个函数的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 的顶点在线段
的顶点在线段![]() 上运动时,形状保持不变,且与
上运动时,形状保持不变,且与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的左侧),给出下列结论:①
的左侧),给出下列结论:①![]() ;②当
;②当![]() 时,
时,![]() 随
随![]() 的增大而增大;③若点
的增大而增大;③若点![]() 的横坐标最大值为
的横坐标最大值为![]() ,则点
,则点![]() 的横坐标最小值为
的横坐标最小值为![]() ;④当四边形
;④当四边形![]() 为平行四边形时,
为平行四边形时,![]() .其中正确的是( )
.其中正确的是( )
A. ②④ B. ②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a=2 002x+2 003,b=2 002x+2 004,c=2 002x+2 005,则多项式a2+b2+c2-ab-bc-ca的值为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程![]() ,下列说法:①若
,下列说法:①若![]() ,则方程必有一根为
,则方程必有一根为![]() ;②若
;②若![]() 是方程
是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;③若
成立;③若![]() ,则方程
,则方程![]() 一定有两个不相等实数根;其中正确结论有( )个.
一定有两个不相等实数根;其中正确结论有( )个.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
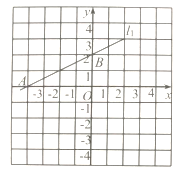
【题目】已知直线l1:y=![]() x+2与x轴交于点A,与y轴交于点B,直线l2:y=-2x+b经过点B且与x轴交于点C.
x+2与x轴交于点A,与y轴交于点B,直线l2:y=-2x+b经过点B且与x轴交于点C.
(1)b=________;(答案直接填写在答题卡的横线上)
(2)画出直线l2的图象;
(3)求△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )

A.60°和135°B.45°、60°、105°、135°C.30°和45°D.以上都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州市处于东南沿海,夏季经常遭受台风袭击.一次,温州气象局测得台风中心在温州市A的正西方向300千米的B处(如图),以每小时10![]() 千米的速度向东偏南30°的BC方向移动,并检测到台风中心在移动过程中,温州市A将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市A的时间会持续多长?( )
千米的速度向东偏南30°的BC方向移动,并检测到台风中心在移动过程中,温州市A将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市A的时间会持续多长?( )

A. 5 B. 6 C. 8 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com