
分析 (1)作AH⊥y轴于点H,如图,根据等边三角形的性质得HF=DH=$\frac{1}{2}$,AH=$\sqrt{3}$HF=$\frac{\sqrt{3}}{2}$,则可得到A点坐标,然后把A点坐标代入y=mx2可求出m的值;
(2)设A(t,t2),利用两点间的距离公式得到AF=t2+$\frac{1}{4}$,则FA=FD=t2+$\frac{1}{4}$,所以D(0,t2+$\frac{1}{2}$),利用待定系数法求出直线l的解析式为y=-$\frac{1}{2t}$x+t2+$\frac{1}{2}$,利用直线平行的问题可设直线l1的解析式为y=-$\frac{1}{2t}$x+a,
接着利用方程-$\frac{1}{2t}$x+a=x2有相等的实数解可求出方程的解得到E(-$\frac{1}{4t}$,$\frac{1}{16{t}^{2}}$),然后利用待定系数法求出直线AE的解析式为y=(t-$\frac{1}{4t}$)x+$\frac{1}{4}$,最后由于x=0时,y=$\frac{1}{4}$,于是可判断直线AE过定点F(0,$\frac{1}{4}$).
解答 解:(1)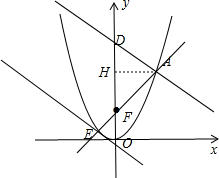 作AH⊥y轴于点H,如图,
作AH⊥y轴于点H,如图,
∵△ADF为正三角形,
∴HF=DH=$\frac{1}{2}$,AH=$\sqrt{3}$HF=$\frac{\sqrt{3}}{2}$,
∴A($\frac{\sqrt{3}}{2}$,$\frac{3}{4}$),
把A($\frac{\sqrt{3}}{2}$,$\frac{3}{4}$)代入y=mx2得m•($\frac{\sqrt{3}}{2}$)2=$\frac{3}{4}$,
∴m=1;
(2)直线AE过定点F.理由如下:
设A(t,t2),则AF=$\sqrt{{t}^{2}+({t}^{2}-\frac{1}{4})^{2}}$=t2+$\frac{1}{4}$,
∵FA=FD,
∴FD=t2+$\frac{1}{4}$,
∴D(0,t2+$\frac{1}{2}$),
设直线l的解析式为y=kx+b,
把D(0,t2+$\frac{1}{2}$),A(t,t2)代入得$\left\{\begin{array}{l}{k=-\frac{1}{2t}}\\{b={t}^{2}+\frac{1}{2}}\end{array}\right.$,
∴直线l的解析式为y=-$\frac{1}{2t}$x+t2+$\frac{1}{2}$,
∵l1∥l,
∴设直线l1的解析式为y=-$\frac{1}{2t}$x+a,
∵l1与抛物线仅交于一点E,
∴方程-$\frac{1}{2t}$x+a=x2有相等的实数解,
∴△=0,x1=x2=-$\frac{1}{4t}$,
∴E(-$\frac{1}{4t}$,$\frac{1}{16{t}^{2}}$),
设直线AE的解析式为y=px+q,
把A(t,t2),E(-$\frac{1}{4t}$,$\frac{1}{16{t}^{2}}$)代入得$\left\{\begin{array}{l}{pt+q={t}^{2}}\\{-\frac{1}{4t}p+q=\frac{1}{16{t}^{2}}}\end{array}\right.$,解得$\left\{\begin{array}{l}{p=t-\frac{1}{4t}}\\{q=\frac{1}{4}}\end{array}\right.$,
∴直线AE的解析式为y=(t-$\frac{1}{4t}$)x+$\frac{1}{4}$,
当x=0时,y=$\frac{1}{4}$,
∴直线AE过定点F(0,$\frac{1}{4}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和等边三角形的性质;会利用待定系数法求二次函数和一次函数的解析式;理解坐标与图形性质,记住两点间的距离公式;能用判别式的值判断抛物线与一次函数的交点个数.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 1<AB<2 | B. | 2<AB<10 | C. | 4<AB<10 | D. | 4<AB<20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.5折 | B. | 8折 | C. | 6折 | D. | 3.3折 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 57 | B. | 73 | C. | 91 | D. | 111 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com