



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 �Ķ���ΪH����
�Ķ���ΪH����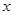 �ύ��A��B���㣨B����A���Ҳࣩ����H��B����ֱ�ߣ�
�ύ��A��B���㣨B����A���Ҳࣩ����H��B����ֱ�ߣ� �Գƣ�����B��ֱ��BK��AH��ֱ����K�㣮����
�Գƣ�����B��ֱ��BK��AH��ֱ����K�㣮����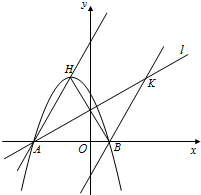 ������������������������������������������������������
�������������������������������������������������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 Ԫ.
Ԫ.
 ��ֵ��
��ֵ�� ����Ԫ��ʱ����Ʒ��������������ԭ������������
����Ԫ��ʱ����Ʒ��������������ԭ������������ ������
������ ��
�� ֮��Ĺ�ϵ����
֮��Ĺ�ϵ����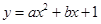 �������ͼ���ṩ����Ϣ�����
�������ͼ���ṩ����Ϣ����� ��
�� ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ�� ����Ԫ��֮��ĺ�����ϵʽ,����ش����
����Ԫ��֮��ĺ�����ϵʽ,����ش���� ����Ԫ����ʲô��Χ�ڣ���˾��õ�������S����Ԫ������ѵ���������ࣿ��ע��������S���������ܶ�ɱ��ѣ����ѣ�
����Ԫ����ʲô��Χ�ڣ���˾��õ�������S����Ԫ������ѵ���������ࣿ��ע��������S���������ܶ�ɱ��ѣ����ѣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
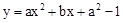 ��ͼ���������ĸ�ͼ֮һ��ʾ������ͼ�������a��ֵ����
��ͼ���������ĸ�ͼ֮һ��ʾ������ͼ�������a��ֵ����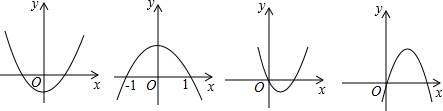
| A����2 | B����1 | C��1 | D��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ���˶�������P��
���˶�������P�� ������ʱ��
������ʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com