已知抛物线y=x2+bx-a2.
(1)请你选定a、b适当的值,然后写出这条抛物线与坐标轴的三个交点,并画出过三个交点的圆;
(2)试讨论此抛物线与坐标轴交点分别是1个,2个,3个时,a、b的取值范围,并且求出交点坐标.
【答案】
分析:(1)要注意选择符合条件的a,b的值,首先要注意确定△>0,-a
2≠0,选择合适的值即可,作图时要注意三角形的外接圆圆心是各边的垂直平分线的交点;
(2)若有一个交点即是与x轴无交点或与x轴的一个交点为原点,
若有两个交点即是与x轴有一个交点,与y轴有一个交点,且不重合;或者与x轴有两个交点且过原点,
若有三个交点即是与两坐标轴都有交点且不重合.
解答: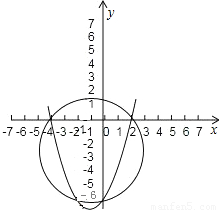
解:(1)∵这条抛物线与坐标轴的三个交点,
∴这条抛物线与x轴的两个交点,
∴△=b
2+4a
2>0且a
2≠0,
∴设b=2,a=
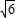
,
∴y=x
2+2x-6,
∴这条抛物线与坐标轴的三个交点为(2,0),(-4,0),(0,-6).
如图:
(2)①当这条抛物线与坐标轴的有一个交点,
∴这条抛物线与坐标轴的交点是原点(0,0),
则a=0,b=0.
②当这条抛物线与坐标轴的有两个交点时,
抛物线过原点,则此时a=0,
∴y=x
2+bx,
交点坐标为(0,0),(-b,0).
③当这条抛物线与坐标轴的有三个交点时,
这条抛物线与x轴交于两点,且不过原点,
∴△=b
2+4a
2>0,
∴a≠0,b为任意实数,
交点坐标为(
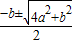
,0),(0,-a
2).
点评:此题考查了二次函数与坐标轴的交点问题的判断,解题的关键是对函数图象的认识,还要注意三角形外接圆的画法;要注意数形结合思想的应用.

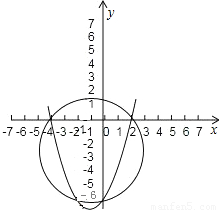 解:(1)∵这条抛物线与坐标轴的三个交点,
解:(1)∵这条抛物线与坐标轴的三个交点,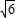 ,
,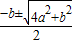 ,0),(0,-a2).
,0),(0,-a2).

 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.