
【题目】数轴上的点![]() 表示的数是5,点
表示的数是5,点![]() 表示的数是
表示的数是![]() ,这两点都以每秒一个单位长度的速度在数轴上各自朝某个方向运动,且两点同时开始运动:
,这两点都以每秒一个单位长度的速度在数轴上各自朝某个方向运动,且两点同时开始运动:
(1)若点![]() 向右运动,则两秒后点
向右运动,则两秒后点![]() 表示的数是_______;(直接写结果)
表示的数是_______;(直接写结果)
(2)若点![]() 向左运动,点
向左运动,点![]() 向右运动,当这两点相遇时点
向右运动,当这两点相遇时点![]() 表示的数是多少?
表示的数是多少?
(3)同时运动3秒后,这两点相距多远?
【答案】(1)7;(2)相遇时点![]() 表示的数为1;(3)这两点的距离为8或2或14.
表示的数为1;(3)这两点的距离为8或2或14.
【解析】
(1)根据运动速度和时间可得运动距离,结合运动方向可得答案;
(2)首先求出相遇时所用的时间,然后再计算相遇时点![]() 表示的数;
表示的数;
(3)分三种情况讨论:①当同时同向运动3秒后,②当点![]() 向左运动,点
向左运动,点![]() 向右运动时,③当点
向右运动时,③当点![]() 向右运动,点
向右运动,点![]() 向左运动时,分别求解即可.
向左运动时,分别求解即可.
解:(1)∵点![]() 表示的数是5,运动速度为每秒一个单位长度,
表示的数是5,运动速度为每秒一个单位长度,
∴若点![]() 向右运动,则两秒后点
向右运动,则两秒后点![]() 表示的数是5+2×1=7,
表示的数是5+2×1=7,
故答案为:7;
(2)由题意得,A、B之间的距离为:5-(-3)=8,
设相遇时所用时间为t,
则t+t=8,
解得:t=4,
∴相遇时点![]() 表示的数为:5-4×1=1;
表示的数为:5-4×1=1;
(3)分三种情况讨论:
①当同时同向运动3秒后,
∵A,B的速度相同,
∴A、B之间的距离不变,为8;
②当点![]() 向左运动,点
向左运动,点![]() 向右运动时,
向右运动时,
A、B之间的距离为:8-3×1-3×1=2;
③当点![]() 向右运动,点
向右运动,点![]() 向左运动时,
向左运动时,
A、B之间的距离为:8+3×1+3×1=14;
综上,同时运动3秒后,这两点的距离为8或2或14.
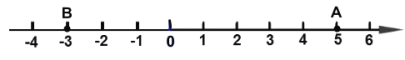


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求梯形ABCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
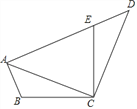
【题目】如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若∠ACB=30°,∠D=45°,求∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)x2+8x-20=0(用配方法);
(2)x2-2x-3=0;
(3)(x-1)(x+2)=4(x-1);
(4)3x2-6x=1(用公式法).
查看答案和解析>>
科目:初中数学 来源: 题型:
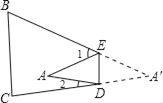
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)设∠AED的度数为x,∠ADE的度数为y,那么∠1、∠2的度数分别是多少?(用含有x或y的代数式表示)
(2)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家需要用钢管做防盗窗,按设计要求,其中需要长为 0.8m,2.5m 且粗细相同的钢管分别为 100 根,32 根,并要求这些用料不能是焊接而成的.现钢材市场的这种规格的钢管每根为 6m.
(1)试问一根 6m 长的圆钢管有哪些裁剪方法呢?请填写下空(余料作废).
方法①:当只裁剪长为 0.8m 的用料时,最多可剪 根;
方法②:当先剪下 1 根 2.5m 的用料时,余下部分最多能剪 0.8m 长的用料 根;
方法③:当先剪下 2 根 2.5m 的用料时,余下部分最多能剪 0.8m 长的用料 根.
(2)分别用(1)中的方法②和方法③各裁剪多少根 6m 长的钢管,才能刚好得到所需要的相应数量的材料?
(3)试探究:除(2)中方案外,在(1)中还有哪两种方法联合,所需要 6m 长的钢管与(2) 中根数相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
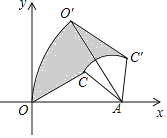
【题目】如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转到△O′AC′,使得点O′的坐标是(1,![]() ),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
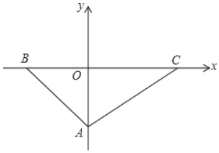
(1)求![]() 三个顶点
三个顶点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,并用含字母
,并用含字母![]() 的式子表示
的式子表示![]() 的面积(
的面积(![]() );
);
(3)在(2)问的条件下,是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积?如果存在,请求出点
的面积?如果存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com