
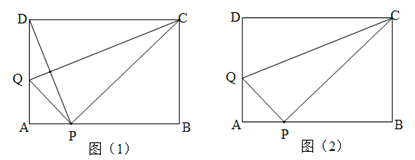
【题目】如图(1)将长方形纸片ABCD的一边CD沿着CQ向下折叠,使点D落在边AB上的点P处.
(1)试判断线段CQ与PD的关系,并说明理由;
(2)如图(2),若AB=CD=5,AD=BC=3.求AQ的长;
(3)如图(2),BC=3,取CQ的中点M,连接MD,PM,若MD⊥PM,求AQ(AB+BC)的值.
【答案】(1)见解析(2)![]() (3)9
(3)9
【解析】
(1)由折叠知CD=CP,∠DCQ=∠PCQ.根据等腰三角形三线合一的性质即可得出结论;
(2)设AQ=x,则DQ=QP=3-x.在Rt△PBC中,由勾股定理可得PB的长,进而得到AP的长.在Rt△APQ中,由勾股定理列方程,求解即可得出结论.
(3)由直角三角形斜边上的中线等于斜边的一半,得到DM=QM=MC=PM,由等腰三角形的性质得到∠MDQ=∠MQD,∠MQP=∠MPQ.再由四边形内角和为360°得到∠DQP=135°,从而得到∠AQP=45°,得到△APQ为等腰直角三角形,从而求出AQ的长.在Rt△PBC中,由勾股定理得到(AB-AQ)2+32=AB2,变形即可得到结论.
(1)CQ垂直平分DP.理由如下:
由折叠的性质可知:CD=CP,∠DCQ=∠PCQ,∴CQ垂直平分DP.
(2)设AQ=x,则DQ=QP=3-x.
∵PC=DC=5,BC=3,∴PB=![]() =4.
=4.
∵AB=5,∴AP=5-4=1.在Rt△APQ中,∵![]() ,∴
,∴![]() ,解得:x=
,解得:x=![]() ,∴AQ=
,∴AQ=![]() .
.
(3)如图,∵∠QDC=∠QPC=90°,M为斜边QC的中点,∴DM=QM=MC=PM,∴∠MDQ=∠MQD,∠MQP=∠MPQ.
∵MD⊥PM,∴∠DMP=90°,∴∠DQP=∠DQM+∠PQM=(360°-90°)÷2=135°,∴∠AQP=180°-135°=45°.
∵∠A=90°,∴∠APQ=∠AQP=45°,∴△APQ时等腰直角三角形,∴AP=AQ,DQ=PQ=![]() AQ.
AQ.
∵AQ+QD=AD=BC=3,∴(![]() +1)AQ=3,解得:AQ=3(
+1)AQ=3,解得:AQ=3(![]() -1)=
-1)=![]() .在Rt△PBC中,∵PB2+BC2=PC2,∴(AB-AQ)2+32=AB2,∴ABAQ=
.在Rt△PBC中,∵PB2+BC2=PC2,∴(AB-AQ)2+32=AB2,∴ABAQ=![]() (AQ2+9),∴AQ(AB+BC)= AQAB+ AQ BC=
(AQ2+9),∴AQ(AB+BC)= AQAB+ AQ BC=![]() (AQ2+9)+3AQ=
(AQ2+9)+3AQ=![]() (AQ+3)2=
(AQ+3)2=![]() =9.
=9.


科目:初中数学 来源: 题型:
【题目】在△ABC和△A′B′C′中,①AB=A′B′,②BC=B′C′,③AC=A′C′,④∠A=∠A′,⑤∠B=∠B′,⑥∠C=∠C′,则下列各组条件中使△ABC和△A′B′C′全等的是( )
A. ④⑤⑥ B. ①②⑥ C. ①③⑤ D. ②⑤⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,求证:AD=DC+AB,
(2)如图②,在四边形ABCD中,AB∥DC,F是DC延长线上一点,连接AF,E是BC的中点,若AE是∠BAF的平分线,求证:AB=AF+CF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如∠MON=30°、OP=6,点A、B分别在OM、ON上;(1)请在图中画出周长最小的△PAB(保留画图痕迹);(2)请求出(1)中△PAB的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y= ![]() 的图象如图,以下结论:
的图象如图,以下结论:
①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
其中正确的个数是( )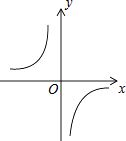
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.

(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
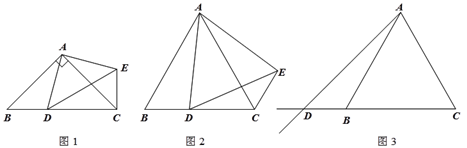
【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC= ![]() ,∠DCE=
,∠DCE= ![]() .
.
① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时![]() 与
与![]() 之间的数量关系(不需证明).
之间的数量关系(不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(a,3),点P在坐标轴上,若使得△AOP是等腰三角形的点P恰有6个,则满足条件的a值有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com