
分析 (1)把给出的式子重新组合,分解因式,分析得出b=c,才能说明这个三角形是等腰三角形.
(2)将等式的左边整理,进一步利用完全平方公式配方,再利用非负数的性质解答即可.
(3)将等式右边的移项到方程左边,然后提取公因式将方程左边分解因式,根据两数相乘积为0,两因式中至少有一个数为0转化为两个等式;根据等腰三角形的判定,得出三角形为等腰三角形.
解答 解:(1)b2+2ab=c2+2ac可变为b2-c2=2ac-2ab,
(b+c)(b-c)=2a(c-b),
(b-c)(b+c+2a)=0,
又知b+c+2a≠0,
即b=c,
所以△ABC为等腰三角形,
(2)∵a2+2b2+c2-2b(a+c)=0,
∴a2-2ab+b2+b2-2bc+c2=0
配方得:(a-b)2+(b-c)2=0
∴a=b=c,
∴△ABC为等边三角形.
(3)∵a4-b2c2=b4-a2c2,
∴-c2(a2-b2)=(a2+b2)(a2-b2),
移项得:c2(a2-b2)-(a2+b2)(a2-b2)=0,
因式分解得:(a2-b2)(c2+a2+b2)=0,
则a2-b2=0,a=b;
所以△ABC是等腰三角形.
点评 此题考查因式分解和勾股定理逆定理的实际运用,掌握平方差公式和完全平方公式是关键.同时考查了等腰三角形的判定,分类讨论思想的应用.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
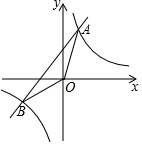 如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$的图象交于A(m,2),B两点.
如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$的图象交于A(m,2),B两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com