练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

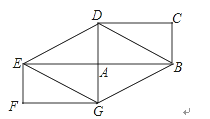
    【题目】如图，矩形ABCD和矩形AEFG关于点A中心对称，

    （1）四边形BDEG是菱形吗？请说明理由．

    （2）若矩形ABCD面积为8，求四边形BDEG的面积．

    【答案】（1）见解析; （2）16．

    【解析】

    （1）直接利用菱形的判定方法得出答案；
    （2）直接利用矩形的面积结合菱形的性质得出答案．

    解：（1）四边形BDEG是菱形．
    ∵矩形ABCD和矩形AEFG关于点A中心对称，
    ∴AB=AE，AD=AG，BE⊥DG，
    ∴根据勾股定理得：BD2=DE2=EG2=GB2=AB2+AD2，
    ∴四边形BDEG是菱形．
    （2）若矩形ABCD面积为8，则S△ABD=SABCD=4，
    ∴根据菱形性质：四边形BDEG的面积为SBDEG=4S△ABD=16．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

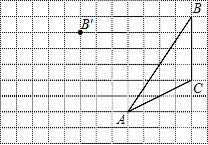
    【题目】画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．利用网格点和三角板画图或计算：

    （1）在给定方格纸中画出平移后的△A′B′C′；

    （2）画出AB边上的中线CD；

    （3）画出BC边上的高线AE；

    （4）△A′B′C′的面积为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y＝ax2＋bx＋c（a≠0）的图象如图所示，则下列结论正确的是

    A.a＜0
    B.c＞0
    C.a＋b＋c＞0
    D.b2－4ac＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

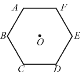
    【题目】如图，点O是正六边形ABCDEF的中心．

    （1）找出这个轴对称图形的对称轴；

    （2）这个正六边形绕点O旋转多少度后能和原来的图形重合？

    （3）如果换成其他的正多边形呢？能得到一般的结论吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O与边BC、AC分别交于D、E两点，过点D作DF⊥AC，垂足为点F．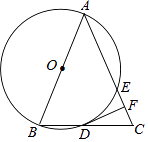
    （1）求证：DF是⊙O的切线；
    （2）若AE=4，cosA= ，求DF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为保护美丽如画的邛海湿地，西昌市污水处理厂决定先购买两型污水处理设备共20台，对湿地周边污水进行处理．每台型污水处理设备12万，每台型污水处理设备10万，已知2台型污水处理设备和1台型污水处理设备每周处理污水680吨，3台型污水处理设备和2台型污水处理设备每周处理污水1120吨．

    （1）求每台、型污水处理设备每周分别可以处理污水多少吨？

    （2）经预算，污水处理厂购买设备的资金不超过230万元，每周处理污水的量不低于4500吨，请列举出所有购买方案，并指出所需购买资金最少的方案及最少资金．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合题
    （1）阅读理解：如图①，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，DC之间的等量关系．

    解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC，得到AB=FC，从而把AB，AD，DC转化在一个三角形中即可判断．
    AB、AD、DC之间的等量关系为；
    （2）问题探究：如图②，在四边形ABCD中，AB∥DC，AF与DC的延长线交于点F，E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论．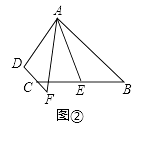

    （3）问题解决：如图③，AB∥CF，AE与BC交于点E，BE：EC=2：3，点D在线段AE上，且∠EDF=∠BAE，试判断AB、DF、CF之间的数量关系，并证明你的结论．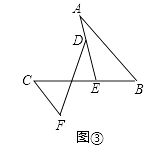

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“2017年张学友演唱会”于6月3日在我市观山湖奥体中心举办，小张去离家2520米的奥体中心看演唱会，到奥体中心后，发现演唱会门票忘带了，此时离演唱会开始还有23分钟，于是他跑步回家，拿到票后立刻找到一辆“共享单车”原路赶回奥体中心，已知小张骑车的时间比跑步的时间少用了4分钟，且骑车的平均速度是跑步的平均速度的1.5倍．
    （1）求小张跑步的平均速度；
    （2）如果小张在家取票和寻找“共享单车”共用了5分钟，他能否在演唱会开始前赶到奥体中心？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC中，AD⊥BC于点D，AE为∠BAC的平分线，且∠B＝36°，∠C＝66°．求∠DAE的度数．

    查看答案和解析>>

    同步练习册答案