
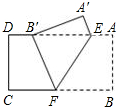
 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上,的点B′处,点A落在点A′处,若AE=6,BF=10,则AB=8.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上,的点B′处,点A落在点A′处,若AE=6,BF=10,则AB=8. 分析 由折叠的性质知:BF=B′F,且∠B′FE=∠BFE,由AD∥BC可知∠B′EF=∠BFE,通过等量代换可证得B′E=B′F=BF,进而可在Rt△A′B′E中,利用勾股定理得到所求线段的关系,代入解答即可.
解答 解:由折叠的性质知:A′B′=AB,AE=A′E,BF=B′F,∠A′=∠A=90°,∠B′FE=∠BFE;
又∵AD∥BC,∴∠BFE=∠B′EF,
∴∠B′EF=∠BFE=∠B′FE,即B′E=B′F=BF;
在Rt△A′B′E中,由勾股定理得:A′B′2+A′E2=B′E2,
即:AE2+AB2=BF2.
∵AE=6,BF=10,
∴AB=$\sqrt{1{0}^{2}-{6}^{2}}=8$.
故答案为:8.
点评 此题考查图形的翻折变换,涉及到矩形的性质、平行线的性质以及勾股定理的综合应用,难度不大.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
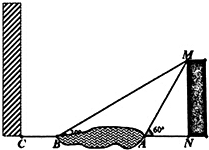 根据《城市居住区规划设计规范》要求,房屋之间的间距不得低于楼高1.2倍.某小区现已建好一幢高60米的住宅楼MN,该楼的背面(即图中楼房的右侧为正面,左侧为背面)有一座小区的景观湖,小丁在景观湖左右两侧各取一点观察该楼楼顶的M点,在A处测得点M的仰角为60°,在B处测得点M的仰角为30°,景观湖的左侧距离B点20米处有一点C,且C、B、A、N都在同一条直线上.
根据《城市居住区规划设计规范》要求,房屋之间的间距不得低于楼高1.2倍.某小区现已建好一幢高60米的住宅楼MN,该楼的背面(即图中楼房的右侧为正面,左侧为背面)有一座小区的景观湖,小丁在景观湖左右两侧各取一点观察该楼楼顶的M点,在A处测得点M的仰角为60°,在B处测得点M的仰角为30°,景观湖的左侧距离B点20米处有一点C,且C、B、A、N都在同一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
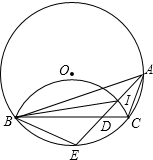 如图,已知△ABC内接于⊙O,点E在弧BC上,AE交BC于点D,EB2=ED•EA经过B、C两点的圆弧交AE于I.
如图,已知△ABC内接于⊙O,点E在弧BC上,AE交BC于点D,EB2=ED•EA经过B、C两点的圆弧交AE于I.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com