
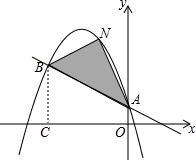
 二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}x$+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).
二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}x$+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).分析 (1)根据直线的解析式为y=-$\frac{1}{2}x$+1可得出点A、点B的坐标,结合给定的坐标(-1,4)利用待定系数法即可求出二次函数解析式;
(2)存在.作AB的平行线EN与抛物线只有一个交点N,交y轴于点E,由直线AB的解析式设出直线EN的解析式为y=-$\frac{1}{2}$x+k,将其代入到二次函数解析式中,根据根的判别式△=0得出关于k的一元一次方程,解方程得出k的值,将k的值代入方程中求出x的值,再将x的值代入到直线EN的解析式中即可求出点N的坐标.
解答 解:(1)令直线y=-$\frac{1}{2}x$+1中x=0,则y=1;
令x=-3,则y=-$\frac{1}{2}$×(-3)+1=$\frac{5}{2}$.
∴点A(0,1),点B(-3,$\frac{5}{2}$).
根据题意可知:$\left\{\begin{array}{l}{c=1}\\{9a-3b+c=\frac{5}{2}}\\{a-b+c=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{5}{4}}\\{b=-\frac{17}{4}}\\{c=1}\end{array}\right.$.
∴二次函数的解析式为:y=-$\frac{5}{4}{x}^{2}$-$\frac{17}{4}$x+1.
(2)存在.
要使△ABN的面积最大,AB长度一定,只要AB上的高最大即可.
作AB的平行线EN与抛物线只有一个交点N,交y轴于点E,如图所示.
此时△ABN的底边AN上的高最大,设直线EN的解析式为y=-$\frac{1}{2}$x+k.
∵y=-$\frac{1}{2}$x+k与抛物线只有一个交点,
∴方程-$\frac{1}{2}$x+k=-$\frac{5}{4}{x}^{2}$-$\frac{17}{4}$x+1,即5x2+15x+4k-4=0的判别式△=152-4×5(4k-4)=0,
解得:k=$\frac{61}{16}$.
∴直线EN的表达式为y=-$\frac{1}{2}$x+$\frac{61}{16}$.
此时方程5x2+15x+4k-4=0变为4x2+12x+9=(2x+3)2=0,
∴x=-$\frac{3}{2}$,
y=-$\frac{1}{2}$×(-$\frac{3}{2}$)+$\frac{61}{16}$=$\frac{73}{16}$.
∴点N的坐标为(-$\frac{3}{2}$,$\frac{73}{16}$).
点评 本题考查了待定系数求二次函数解析式以及根的判别式,解题的关键是:(1)求出点A、点B的坐标;(2)求出直线EN的解析式.本题属于基础题,难度不大,解决该题型题目时,结合三角形的面积公式通过直线与抛物线相切来求极值是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,A,B两地之间有一座山,汽车原来从A地道B地须经C地沿折线A-C-B行驶,全长68km,现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,A,B两地之间有一座山,汽车原来从A地道B地须经C地沿折线A-C-B行驶,全长68km,现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
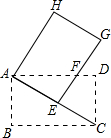 将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )
将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )| A. | 2 | B. | $\frac{7}{4}$ | C. | $\frac{9}{4}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
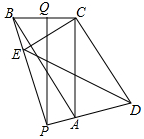 如图,△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD、EB交于P点,Q是BC的中点,连PQ在旋转过程中,PQ最大值是( )
如图,△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD、EB交于P点,Q是BC的中点,连PQ在旋转过程中,PQ最大值是( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2x-1)(2x-1)=1-4x2 | B. | 2x(x2-2x-14)=2x3-4x2+28x | ||
| C. | (x-2y)2=x2-2xy+4y2 | D. | (x+1)(x-4)=x2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3,b=4,c=5 | B. | a=2$\sqrt{13}$,b=3,c=$\sqrt{43}$ | C. | a=12,b=10,c=20 | D. | a=5,b=13,c=12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com