
【题目】阅读材料:
把代数式通过配凑等手段得到局部完全平方式,再进行有关计算和解题,这种解题方法叫做配方法.
如(1)用配方法分解因式:![]() .
.
解:原式=![]()
=![]()
(2)M=![]() ,利用配方法求M的最小值.
,利用配方法求M的最小值.
解:M=![]()
=![]()
![]()
![]() M有最小值1.
M有最小值1.
请根据上述材料,解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:![]()
(2)用配方法分解因式:![]()
(3)若M=![]() ,求M的最小值.
,求M的最小值.
科目:初中数学 来源: 题型:
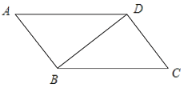
【题目】如图,已知![]() 为
为![]() 的一条对角线.
的一条对角线.
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母;(保留作图痕迹,不写作法)
①作![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,交
两点,交![]() 于点
于点![]() ;
;
②连接![]() ,
,![]() ;
;
(2)猜想与证明:试猜想四边形![]() 是哪种特殊的四边形,并说明理由.
是哪种特殊的四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )

A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
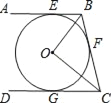
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。

(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
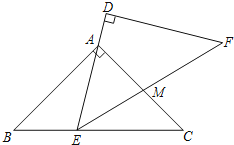
【题目】△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=![]() .现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.
.现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作发现:
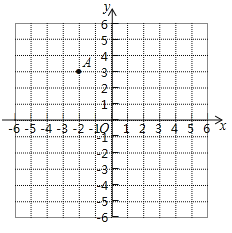
(1)如图,在平面直角坐标系中有一点![]() ,将点
,将点![]() 先向右平移3个单位长度,再向下平移3个单位长度得到点
先向右平移3个单位长度,再向下平移3个单位长度得到点![]() ,则点
,则点![]() 的坐标为 ;并在图中画出直线
的坐标为 ;并在图中画出直线![]() 的函数图象;
的函数图象;
(2)直接写出直线![]() 的解析式 ;
的解析式 ;
(3)若直线![]() 上有一动点
上有一动点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①直接写出点![]() 的坐标 ;
的坐标 ;
②若点![]() 位于第四象限,直接写出三角形
位于第四象限,直接写出三角形![]() 的面积 .(用含
的面积 .(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com