
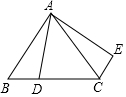
 如图,在等边三角形ABC中,AB=2,动点D从B开始沿BC向点C运动,到达点C后停止运动,将△ABD绕点A旋转后得到△ACE,则下列说法中,正确的是( )
如图,在等边三角形ABC中,AB=2,动点D从B开始沿BC向点C运动,到达点C后停止运动,将△ABD绕点A旋转后得到△ACE,则下列说法中,正确的是( )| A. | ①③④ | B. | ①②③ | C. | ②③④ | D. | ①②④ |
分析 根据旋转的性质和全等三角形的判定以及等边三角形的性质进行判断即可.
解答 解:当BD=DC时,DE有最小值,
∵△ABC为等边三角形,
∴AB=BC=2,∠B=∠BAC=60°,
∵D是BC的中点,即BD=DC=$\frac{1}{2}$BC=1,
∴AD⊥BC,∠BAD=30°,
∴AD=$\sqrt{3}$BD=$\sqrt{3}$,
∵△ABD绕点A旋转后得到△ACE,
∴∠DAE=∠BAC=60°,AD=AE,
∴△ADE为等边三角形,
∴DE=AD=$\sqrt{3}$,
故①错误;
∵将△ABD绕点A旋转后得到△ACE,
∴△ABD的面积=△ACE的面积,
∴ADCE的面积=等边三角形ABC的面积不变,
故②正确;
在整个运动过程中,点E运动的路程等于等边三角形的边长即为2,
故③正确;
在整个运动过程中,△ADE的周长先变小后变大,正确;
故选C
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质和含30度的直角三角形三边的关系.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
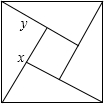 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),请观察图案,指出以下关系式中不正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),请观察图案,指出以下关系式中不正确的是( )| A. | x2+y2=49 | B. | x-y=2 | C. | 2xy+4=49 | D. | x+y=9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=(x+2)2 | C. | y=x2+4 | D. | y=(x+2)2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
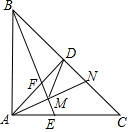 如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①AE=AF;②AM⊥EF;③AF=DF;④DF=DN,其中正确的结论有( )
如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①AE=AF;②AM⊥EF;③AF=DF;④DF=DN,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个角和一条边对应相等的两个三角形全等 | |
| B. | 有一条边和一个锐角对应相等的两个直角三角形全等 | |
| C. | 有两边和其中一边的对角对应相等的两个三角形全等 | |
| D. | 有两条直角边对应相等的两个直角三角形全等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com