
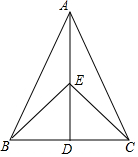
 如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )
如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )| A. | △ABD≌△ACE | B. | △ABE≌△ACE | C. | △BDE≌△CDE | D. | △ABD≌△ACD |
分析 根据AB=AC,EB=EC可得AE是BC的垂直平分线,进而可得BD=CD,然后利用全等三角形的判定方法分别进行分析即可.
解答 解:∵AB=AC,
∴A在BC的垂直平分线上,
∵EB=EC,
∴E在BC的垂直平分线上,
∴AE是BC的垂直平分线,
∴BD=CD,
在△ABD和△ACD中$\left\{\begin{array}{l}{AD=AD}\\{BD=CD}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACD(SSS),故A判断错误,D判断正确;
在△ABE和△ACE中$\left\{\begin{array}{l}{AB=AC}\\{BE=CE}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△ACE(SSS),故B判断正确;
在△BED和△CED中$\left\{\begin{array}{l}{ED=ED}\\{BE=CE}\\{DB=DC}\end{array}\right.$,
∴△BED≌△CED(SSS),故C判断正确;
故选:A.
点评 本题考查三角形全等的判定方法,以及线段垂直平分线的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,数轴上顺次有A、B、D、E、P、C六个点,且任意相邻两点之间的距离都相等,点A、B、C对应的数分别为a、b、c,下列说法:①若a+b+c=0,则D为原点;②若|c|>|a|>|b|,则原点在B、D之间;③若c-b=8,则a-b=-2;④若原点在D、E之间,则|a+b|<2c,其中正确的结论有( )
如图,数轴上顺次有A、B、D、E、P、C六个点,且任意相邻两点之间的距离都相等,点A、B、C对应的数分别为a、b、c,下列说法:①若a+b+c=0,则D为原点;②若|c|>|a|>|b|,则原点在B、D之间;③若c-b=8,则a-b=-2;④若原点在D、E之间,则|a+b|<2c,其中正确的结论有( )| A. | ①②③ | B. | ①③ | C. | ③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,等边△ABC的顶点B,C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M,当点M恰平分线段ON时,求线段CN的长.
如图,在平面直角坐标系中,等边△ABC的顶点B,C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M,当点M恰平分线段ON时,求线段CN的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)用适当的方法解下列一元二次方程:x2-6x+1=0.
(1)用适当的方法解下列一元二次方程:x2-6x+1=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
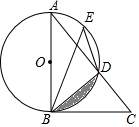 如图所示,AB是⊙O的直径,BC与⊙O相切,切点为B,AC与⊙O相交于点D,点E是$\widehat{AD}$上任一点.
如图所示,AB是⊙O的直径,BC与⊙O相切,切点为B,AC与⊙O相交于点D,点E是$\widehat{AD}$上任一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com