
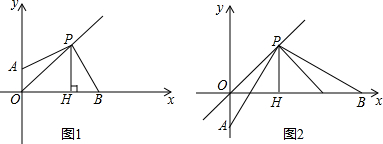
分析 (1)过点P作PN⊥AO于N.则∠PNA=90°,由P在直线y=x上,得出PH=PN.得出四边形PNOH是正方形,得出PN=ON=OH=PH,∠NPH=90°,由ASA证明△APN≌△BPH,得出AN=BH,PA=PB,即可得出OA+OB=2PH;
(2)过点P作PN⊥AO于N,同(1)得:四边形PNOH是正方形,△APN≌△BPH,得出PN=ON=OH=PH,AN=BH,PA=PB,即可得出结论;
(3)作DM⊥PB于M,则∠DMB=90°,由含30°角的直角三角形的性质得出DM=$\frac{1}{2}$BD=4,BM=$\sqrt{3}$DM=4$\sqrt{3}$,由等腰直角三角形的性质得出PM=DM=4,得出PB=PA=4+4$\sqrt{3}$,求出PN,NA,ON,再求出OA=NA-ON=4,即可得出点A的坐标.
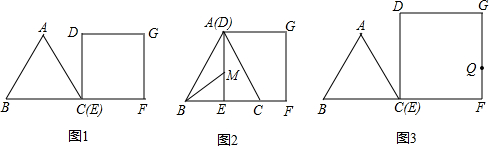
解答 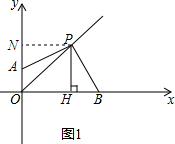 (1)解:过点P作PN⊥AO于N.如图1所示:
(1)解:过点P作PN⊥AO于N.如图1所示:
则∠PNA=90°,
∵P在直线y=x上,
∴PH=PN.
∵PH⊥OB,
∴∠PHO=∠PHB=90°,
∴四边形PNOH是正方形,
∴PN=ON=OH=PH,∠NPH=90°,
∵PB⊥PA,
∴∠APB=90°,
∴∠APN=∠BPH,
在△APN和△BPH中,
$\left\{\begin{array}{l}{∠PNA=∠PHB}&{\;}\\{PN=PH}&{\;}\\{∠APN=∠BPH}&{\;}\end{array}\right.$,
∴△APN≌△BPH(ASA),
∴AN=BH,PA=PB,
∴OA+OB=OA+OH+BH=OA+PH+AN=ON+PH=2PH;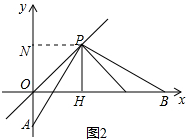
故答案为:OA+OB=2PH;
(2)证明:过点P作PN⊥AO于N,如图2所示
同(1)得:四边形PNOH是正方形,△APN≌△BPH(ASA),
∴PN=ON=OH=PH,AN=BH,PA=PB,
∴OB-OA=OH+BH-OA=OH+AN-OA=OH+ON=2PH;
(3)解:作DM⊥PB于M,如图3所示: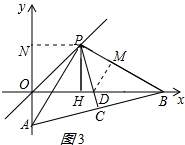
则∠DMB=90°,
∵∠OBP=30°,
∴DM=$\frac{1}{2}$BD=4,BM=$\sqrt{3}$DM=4$\sqrt{3}$,
∵PA=PB,PC⊥AB,
∴∠DPB=45°,
∴PM=DM=4,
∴PB=4+4$\sqrt{3}$,
∴PA=4+4$\sqrt{3}$,
∵∠PAN=30°,
∴PN=2+2$\sqrt{3}$,NA=2$\sqrt{3}$+6,
∴ON=2$+2\sqrt{3}$,
∴OA=NA-ON=4,
∴点A的坐标为(0,-4).
点评 本题是一次函数综合题目,考查了全等三角形的判定与性质、正方形的判定与性质、一次函数的性质、含30°角的直角三角形的性质、等腰直角三角形的判定与性质等知识;本题综合性强,难度适中.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
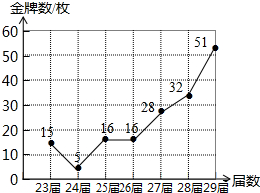 从1984年起,我国先后参加了第23届夏季奥运会,取得了骄人的成绩.如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图,观察统计图可得:与上一届相比增长量最大的是第29届夏季奥运会,比它的上一届增加了19枚金牌.
从1984年起,我国先后参加了第23届夏季奥运会,取得了骄人的成绩.如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图,观察统计图可得:与上一届相比增长量最大的是第29届夏季奥运会,比它的上一届增加了19枚金牌.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
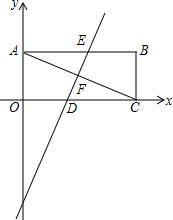 如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4.
如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
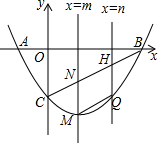 如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线x=m(m>0),直线x=n(n>0)(m<n)分别交线段BC于N点、H点,交抛物线于M点、Q点.当NH∥MQ时,求m+n的值.
如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线x=m(m>0),直线x=n(n>0)(m<n)分别交线段BC于N点、H点,交抛物线于M点、Q点.当NH∥MQ时,求m+n的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com