
 如图所示,在一个半径为R的均匀圆形薄金属片上挖去一个半径为
如图所示,在一个半径为R的均匀圆形薄金属片上挖去一个半径为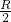 的小圆孔,且圆孔跟圆板的边缘相切,求剩余部分的重心位置.
的小圆孔,且圆孔跟圆板的边缘相切,求剩余部分的重心位置.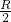 )2hρg=
)2hρg= πR2hρg
πR2hρg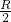 的小圆孔,必须在它的对应位置(左边)填上一个半径为
的小圆孔,必须在它的对应位置(左边)填上一个半径为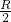 的小圆孔,
的小圆孔,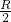 )2hρg=
)2hρg= πR2hρg,重心在O2上,且OO2=
πR2hρg,重心在O2上,且OO2=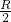 ,如图乙,
,如图乙, πR2hρg•(
πR2hρg•(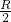 -OO′)=
-OO′)= πR2hρg•OO′,解得OO′=
πR2hρg•OO′,解得OO′=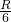 .
.
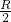 )2hρg=
)2hρg= πR2hρg
πR2hρg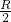 的小圆孔,必须在它的对应位置(左边)填上一个半径为
的小圆孔,必须在它的对应位置(左边)填上一个半径为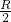 的小圆孔,则它的重力为G2=
的小圆孔,则它的重力为G2= πR2hρg,重心在O2上,OO2=
πR2hρg,重心在O2上,OO2=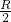 ,设挖孔后的圆片的重心在O′点,经过上面的这一“挖”一“填”,再将1和2综合在一起,就等效于以O′为支点的杠杆,由杠杆的平衡条件知,G2•O2O=G•OO′,求得OO′的值即可.
,设挖孔后的圆片的重心在O′点,经过上面的这一“挖”一“填”,再将1和2综合在一起,就等效于以O′为支点的杠杆,由杠杆的平衡条件知,G2•O2O=G•OO′,求得OO′的值即可.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源:《第24章 圆(下)》2010年综合复习测试(二)(解析版) 题型:解答题
 的小圆孔,且圆孔跟圆板的边缘相切,求剩余部分的重心位置.
的小圆孔,且圆孔跟圆板的边缘相切,求剩余部分的重心位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com