

分析 (1)根据题中的例子即可直接得出结论;
(2)根据直角三角形的性质得出CO=a+b,CD=$\sqrt{ab}$,再由(1)中的结论即可得出等号成立时的条件;
(3)过点A作AH⊥x轴于点H,根据S四边形ADFE=S△ADE+S△FDE可知当DH=EH时DE最小,由此可得出结论.
解答 解:(1)∵a+b≥2$\sqrt{ab}$,a、b均为正实数,
∴当且仅当a、b满足a=b时,a+b有最小值.
故答案为:a=b;
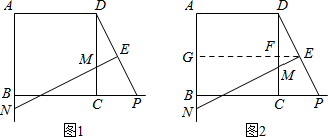
(2)∵△ABC中,∠ACB=90°,CD⊥AB,CO为AB边上中线,AD=2a,DB=2b,
∴OC=$\frac{1}{2}$(AD+BD)=a+b,CD=2$\sqrt{ab}$,OC≥CD,即a+b≥2$\sqrt{ab}$,
∴当点D与点O重合时等式成立;
(3)如图所示,过点A作AH⊥x轴于点H,
∵S四边形ADFE=S△ADE+S△FDE=$\frac{1}{2}$DE•|yA|+$\frac{1}{2}$DE•OF=$\frac{1}{2}$DE(yA+OF),
∴当DH=EH时DE最小,
∴A点的横坐标为1,
∴AH=4,
∴DE最小为8,
∴S四边形ADFE=$\frac{1}{2}$×8×(4+3)=28.
点评 本题考查的是反比例函数综合题,涉及到用配方法可求最大(小)值,在a+b≥2$\sqrt{ab}$(a、b均为正实数)中,若ab为定值,则当且仅当a、b满足a=b时,a+b有最小值2$\sqrt{ab}$是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
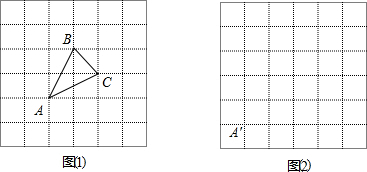
 如图,在△ABC中,AD是角平分线,点E在AB上,且DE∥CA.
如图,在△ABC中,AD是角平分线,点E在AB上,且DE∥CA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
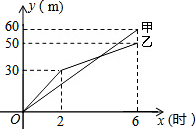 在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com