
【题目】如图,有一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成,隧道最大高度为4.9米,AB=10米,BC=2.4米,若有一辆高为4米、宽为2米的集装箱的汽车要通过隧道,为了使箱顶不碰到隧道顶部,又不违反交通规则(汽车应靠道路右侧行驶,不能超过道路中线),汽车的右侧必须离开隧道右壁几米?
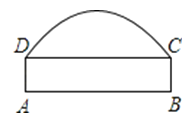
【答案】2米.
【解析】
以AB为x轴,其中点为坐标原点建立平面直角坐标系,则B点坐标为(5,0),E点坐标为(0,4.9),C点坐标为(5,2.4),求得抛物线解析式,进一步利用图象上的点解答即可.
如图,建立平面直角坐标系,
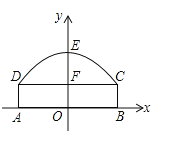
由题意知,B点坐标为(5,0),E点坐标为(0,4.9),C点坐标为(5,2.4),
设抛物线解析式为y=ax2+4.9,代入C点
解得a=﹣0.1,
因此抛物线解析式为y=﹣0.1x2+4.9;
当汽车高4米,代入抛物线的解析式y=﹣0.1x2+4.9,
解得x=±3(舍去负值),
∴x=3,
5﹣3=2,
即车右侧到中线的水平距离为3米.则汽车的右侧离开隧道右壁2米才不至于碰到隧道顶部.
答:汽车的右侧离开隧道右壁2米才不至于碰到隧道顶部.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,
,![]() .
.
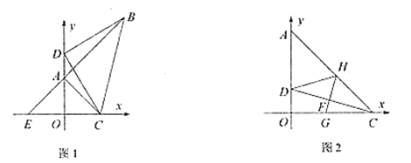
(1)若![]() ,
,![]() 满足
满足![]() .
.
①直接写出![]() ______,
______,![]() ______.
______.
②如图1,![]() 为点
为点![]() 上方一点,连接
上方一点,连接![]() ,在
,在![]() 轴右侧作等腰
轴右侧作等腰![]() ,
,![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,当点
,当点![]() 上方运动时,求
上方运动时,求![]() 的面积;
的面积;
(2)如图2,若![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .连接
.连接![]() ,当
,当![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB⊥AC,DE⊥AB,AC=BE,BC=BD,

(1)求证:BC⊥BD;
(2)若点F是BC,BD的垂直平分线的交点,连接FA、FE.填空:判断△AFE的形状是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是半圆
是半圆![]() 上的一点,
上的一点,![]() 平分
平分![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
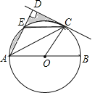
![]() 判断
判断![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
![]() 若
若![]() 是
是![]() 的中点,
的中点,![]() 的半径为
的半径为![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O在等边△ABC内,∠BOC=150°,将△BOC绕点C顺时针旋转后,得△ADC,连接OD.
(1)△COD是______三角形.
(2)若OB=5,OC=3,求OA的长.
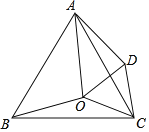
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接省一级示范学校的验收,广安二中决定对学校校园内的环校跑道进行改造,需要铺设一条长为4200米的道路,根据招标文件得知甲工程队比乙工程队每天能多铺设20米.甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
![]() 甲、乙工程队每天各能铺设多少米?
甲、乙工程队每天各能铺设多少米?
![]() 施工时,需付给甲队每天施工费3000元,需付给乙队每天施工费2500元,单独承包给甲队或乙队,或者两队一起施工都可以,但为了节约经费,方便全校师生出行,聪明的同学们你认为三种承包方式怎样承包最合理?
施工时,需付给甲队每天施工费3000元,需付给乙队每天施工费2500元,单独承包给甲队或乙队,或者两队一起施工都可以,但为了节约经费,方便全校师生出行,聪明的同学们你认为三种承包方式怎样承包最合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=![]() S△ABP,其中正确的是( )
S△ABP,其中正确的是( )

A.①③B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】模型发现:
同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.
因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.
特别的,当点C位于 时,线段BC的长取得最大值,且最大值为 (用含b,c的式子表示)(直接填空)
模型应用:
点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接BD,AE.
(1)求证:BD=AE.
(2)线段AE长的最大值为 .
模型拓展:
如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB=8.若AC⊥AB,AC=3,试求OC长的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com