
【题目】如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且AB=1,OB=![]() ,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
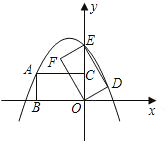
(1)判断点E是否在y轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在x轴的上方是否存在点P,点Q,使以点O,B,P,Q为顶点的平行四边形的面积是矩形ABOC面积的2倍,且点P在抛物线上?若存在,请求出点P,点Q的坐标;若不存在,请说明理由.
【答案】(1)在;(2)![]() ;(3)当点P1的坐标为(0,2)时,点Q的坐标分别为Q1(-
;(3)当点P1的坐标为(0,2)时,点Q的坐标分别为Q1(-![]() ,2),Q2(
,2),Q2(![]() ,2);当点P2的坐标为(-
,2);当点P2的坐标为(-![]() ,2)时,点Q的坐标分别为Q3(-
,2)时,点Q的坐标分别为Q3(-![]() ,2),Q4(
,2),Q4(![]() ,2).
,2).
【解析】
(1)可连接OA,通过证∠AOE=60°,即与旋转角相同来得出OE在y轴上的结论.
(2)已知了AB,OB的长即可求出A的坐标,在直角三角形OEF中,可用勾股定理求出OE的长,也就能求得E点的坐标,要想得出抛物线的解析式还少D点的坐标,可过D作x轴的垂线,通过构建直角三角形,根据OD的长和∠DOx的正弦和余弦值来求出D的坐标.
求出A、E、D三点坐标后即可用待定系数法求出抛物线的解析式.
(3)可先求出矩形的面积,进而可得出平行四边形OBPQ的面积.由于平行四边形中OB边的长是定值,因此可根据平行四边形的面积求出P点的纵坐标(由于P点在x轴上方,因此P的纵坐标为正数),然后将P点的纵坐标代入抛物线中可求出P点的坐标.求出P点的坐标后,将P点分别向左、向右平移OB个单位即可得出Q点的坐标,由此可得出符合条件的两个P点坐标和四个Q点坐标.
(1)点E在y轴上
理由如下:
连接AO,如图所示,在Rt△ABO中,∵AB=1,BO=![]() ,
,
∴AO=2∴sin∠AOB=![]() ,∴∠AOB=30°
,∴∠AOB=30°
由题意可知:∠AOE=60°∴∠BOE=∠AOB+∠AOE=30°+60°=90°
∵点B在x轴上,∴点E在y轴上.
(2)过点D作DM⊥x轴于点M,

∵OD=1,∠DOM=30°
∴在Rt△DOM中,DM=![]() ,OM=
,OM=![]()
∵点D在第一象限,
∴点D的坐标为(![]() ,
,![]() )
)
由(1)知EO=AO=2,点E在y轴的正半轴上
∴点E的坐标为(0,2)
∴点A的坐标为(-![]() ,1)
,1)
∵抛物线y=ax2+bx+c经过点E,
∴c=2
由题意,将A(-![]() ,1),D(
,1),D(![]() ,
,![]() )代入y=ax2+bx+2中,
)代入y=ax2+bx+2中,
得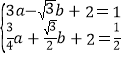
解得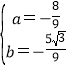
∴所求抛物线表达式为:y=-![]() x2-
x2-![]() x+2
x+2
(3)存在符合条件的点P,点Q.
理由如下:∵矩形ABOC的面积=ABBO=![]()
∴以O,B,P,Q为顶点的平行四边形面积为2![]() .
.
由题意可知OB为此平行四边形一边,
又∵OB=![]()
∴OB边上的高为2
依题意设点P的坐标为(m,2)
∵点P在抛物线y=-![]() x2-
x2-![]() x+2上
x+2上
∴-![]() m2-
m2-![]() m+2=2
m+2=2
解得,m1=0,m2=-![]()
∴P1(0,2),P2(-![]() ,2)
,2)
∵以O,B,P,Q为顶点的四边形是平行四边形,
∴PQ∥OB,PQ=OB=![]() ,
,
∴当点P1的坐标为(0,2)时,点Q的坐标分别为Q1(-![]() ,2),Q2(
,2),Q2(![]() ,2);
,2);
当点P2的坐标为(-![]() ,2)时,点Q的坐标分别为Q3(-
,2)时,点Q的坐标分别为Q3(-![]() ,2),Q4(
,2),Q4(![]() ,2).
,2).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,点A在y轴的正半轴上,点B在x轴的负半轴上,点C是线段AB上一动点CD⊥y轴于点D,CE⊥x轴于点E,OA=6,AD=OE.
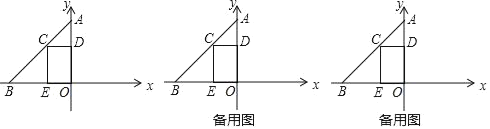
(1)求直线AB的解析式;
(2)连接ED,过点C作CF⊥ED,垂足为F,过点B作x轴的垂线交FC的延长线于点G,求点G的坐标;
(3)在(2)的条件下,连接AG,作四边形AOBG关于y轴的对称图形四边形AONM,连接DN,将线段DN绕点N逆时针旋转90°得到线段PN,H为OD中点,连接MH、PH,四边形MHPN的面积为40,连接FH,求线段FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子中有1个白球和2个红球,这些球除颜色外都相同.
⑴如果从盒子中随机摸出1个球,摸出红色球的概率为_____________;
⑵若从盒子中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,请通过列表或画树状图的方法,求两次摸到不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
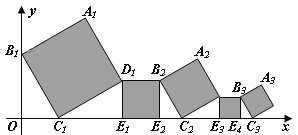
【题目】如图,在平面直角坐标系中放置5个正方形,点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O﹦60,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
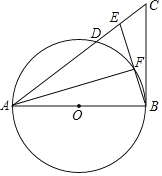
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:EF=BF;
(2)求证:BC是⊙O的切线.
(3)若AB=4,BC=3,求DE的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
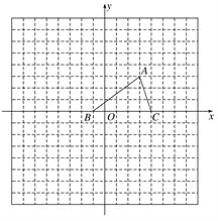
【题目】如图,已知△ABC的三个顶点的坐标分别为A(3,3)、B(-1,0)、C(4,0).
(1)经过平移,可使△ABC的顶点A与坐标原点O重合,请直接写出此时点C的对应点C1坐标;(不必画出平移后的三角形)
(2)将△ABC绕点B逆时针旋转90°,得到△A′BC′,画出△A′BC′并写出A′点的坐标;
(3)以点A为位似中心放大△ABC,得到△AB2C2,使放大前后的面积之比为1∶4,请你在网格内画出△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,AB=4,∠DAB=120°,动点P从点A出发,以每秒2个单位的速度沿AC向终点C运动.过P作PE⊥AB交AB于点E,作PF⊥AD交AD于点F,设四边形AEPF与△ABD的重叠部分的面积为S,点P的运动时间为t.
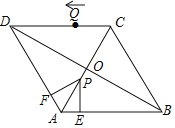
(1)用含t的代数式表示线段BE的长;
(2)当点P与点O重合时,求t的值;
(3)求S与t之间的函数关系式;
(4)在点P出发的同时,有一点Q从点C出发,以每秒6个单位的速度沿折线C﹣D﹣A﹣B运动,设点Q关于AC的对称点是Q',直接写出PQ'与菱形ABCD的边垂直时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com