
【题目】如图,将直角三角形ABC绕其直角顶点C顺时针旋转至△A′B′C′,已知AC=8,BC=6,点M,M′分别是AB,A′B′的中点,则MM′的长是( )

A. 5![]() B. 4 C. 3 D. 5
B. 4 C. 3 D. 5
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y=kx(x≥0)与反比例函数y= ![]() 的图象交于点A(2,3),
的图象交于点A(2,3), 
(1)求k,m的值;
(2)写出正比例函数值大于反比例函数值时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
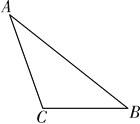
【题目】如图,在△ABC中,∠B=38°,∠C=112°.(1)按下列要求作图:(保留作图痕迹)
①BC边上的高AD;
②∠A的平分线AE.
(2)求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠BAC=∠ABD=90°,AC=BD,点O是AD,BC的交点,点E是AB的中点.
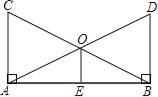
(1)图中有哪几对全等三角形?请写出来;
(2)试判断OE和AB的位置关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
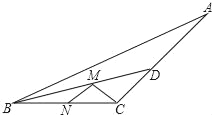
【题目】如图,钝角三角形△ABC的面积是15,最长边AB=10,BD平分∠ABC,点M,N分别是BD,BC上的动点,则CM+MN的最小值为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为______,图2中阴影部分面积为_____,对照两个图形的面积可以验证________公式(填公式名称)请写出这个乘法公式________.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元,小彬从该网店购买了3筒甲种羽毛球和2筒乙种羽毛球,一共花费270元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定购进甲、乙两种羽毛球各80筒.已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.元旦期间该网店开展优惠促销活动,甲种羽毛球打折销售,乙种羽毛球售价不变,若所购进羽毛球均可全部售出,要使全部售出所购进的羽毛球的利润率是![]() ,那么甲种羽毛球是按原销售价打几折销售的.
,那么甲种羽毛球是按原销售价打几折销售的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com