
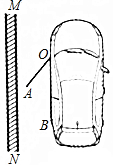
 如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米.已知小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin40°≈0.64;cos40°≈0.77;tan40°≈0.84)
如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米.已知小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin40°≈0.64;cos40°≈0.77;tan40°≈0.84)  小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 186,188 | B. | 188,187 | C. | 187,188 | D. | 188,186 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若一组数据是1,2,3,4,5,则它的方差是3 | |
| B. | 若分式方程$\frac{4}{{({x+1})({x-1})}}-\frac{m}{x-1}=1$有增根,则它的增根是1 | |
| C. | 对角线互相垂直的四边形,顺次连接它的四边中点所得四边形是菱形 | |
| D. | 若一个角的两边分别与另一个角的两边平行,则这两个角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com