
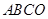 的边
的边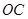 落在
落在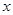 轴的正半轴上,且
轴的正半轴上,且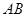 ∥
∥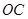 ,
,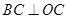 ,
,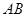 =4,
=4,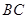 =6,
=6,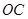 =8.正方形
=8.正方形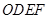 的两边分别落在坐标轴上,且它的面积等于直角梯形
的两边分别落在坐标轴上,且它的面积等于直角梯形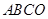 面积。将正方形
面积。将正方形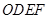 沿
沿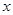 轴的正半轴平行移动,设它与直角梯形
轴的正半轴平行移动,设它与直角梯形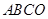 的重叠部分面积为
的重叠部分面积为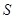 。
。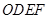 的边长;
的边长;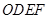 平行移动过程中,通过操作、观察,试判断
平行移动过程中,通过操作、观察,试判断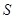 (
(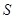 >0)的变化情况是 ;
>0)的变化情况是 ;| A.逐渐增大 | B.逐渐减少 | C.先增大后减少 | D.先减少后增大 |
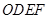 顶点
顶点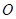 移动到点
移动到点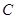 时,求
时,求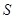 的值;
的值;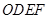 的顶点
的顶点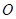 向右移动的距离为
向右移动的距离为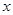 ,求重叠部分面积
,求重叠部分面积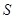 与
与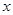 的函数关系式。
的函数关系式。
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源:不详 题型:解答题
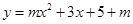 与x轴交于A、B两点(点A
与x轴交于A、B两点(点A 相似?若存在,请求出点F的坐标,若不存在,请说明理由;
相似?若存在,请求出点F的坐标,若不存在,请说明理由;  ?若存在,求出点G的坐标;若不存在,请说明理由.
?若存在,求出点G的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
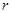 的⊙
的⊙ ,对于任意点
,对于任意点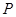 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
·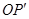 =
=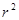 ,这种把点
,这种把点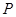 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点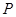 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.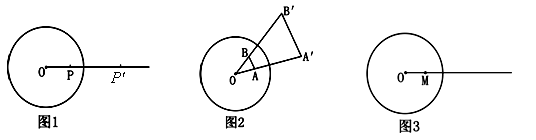
 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是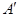 、
、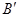 ,则与∠
,则与∠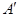 一定相等的角是( ▲ )
一定相等的角是( ▲ )A.∠ | B.∠ | C.∠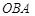 | D.∠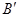 |
 内有一点
内有一点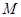 ,请用尺规作图画出点
,请用尺规作图画出点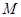 的反演点
的反演点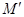 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法). 的半径为
的半径为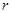 ,另一个半径为
,另一个半径为 的⊙
的⊙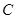 ,作射线
,作射线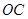 交⊙
交⊙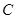 于点
于点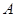 、
、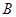 ,点
,点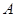 、
、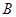 关于⊙
关于⊙ 的反演点分别是
的反演点分别是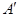 、
、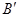 ,点
,点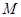 为⊙
为⊙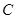 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为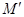 .求证:∠
.求证:∠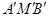 =90°.
=90°.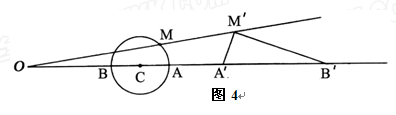
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
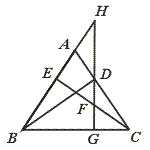
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
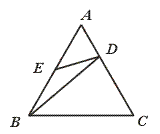
 =
=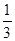 ,AE=BE,则有………………………………………………………………………………………( )
,AE=BE,则有………………………………………………………………………………………( )| A.△AED∽△BED | B.△AED∽△CBD |
| C.△AED∽△ABD | D.△BAD∽△BCD |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com