
 如图所示,在△ABC中,AD为BC边上的中线,且AD平分∠BAC,求证:AB=AC.
如图所示,在△ABC中,AD为BC边上的中线,且AD平分∠BAC,求证:AB=AC. 分析 作DF⊥AB,DE⊥AC,根据三角形的角平分线性质,可得DF=DE,根据“HL”定理,易证Rt△BDE≌Rt△CDF,即可证得.
解答 证明:如图,作DF⊥AB,DE⊥AC,
∵AD平分∠BAC,
∴DE=DF,∠BFD=∠CED=90°,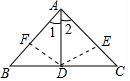
∵D是BC的中点,
∴BD=CD,
在Rt△BDF和Rt△CDE中,
$\left\{\begin{array}{l}{DF=DE}\\{BD=CD}\end{array}\right.$,
∴Rt△BDF≌Rt△CDE(HL),
∴∠B=∠C,
∴AB=AC.
点评 本题主要考查了全等三角形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具,在判定三角形全等时,关键是选择恰当的判定条件.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一次右拐60°,第二次左拐120° | B. | 第一次左拐60°,第二次右拐60° | ||
| C. | 第一次左拐60°,第二次左拐120° | D. | 第一次右拐60°,第二次右拐60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
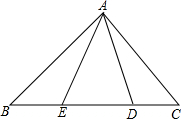 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB).
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE.
如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com