
����Ŀ���Ķ��������ݣ�����Ҫ�������⣺ ���⣺����ƽ���ڣ���֪�ֱ���![]() ���㣬
���㣬![]() ���㣬
���㣬![]() ���㣬5 ���㣬����n ���㣬���������� ���㶼����ͬһ��ֱ����.����ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ� �� ̽����Ϊ�˽��������⣬ϣ��С���ͬѧ����������±������̽������Ϊ�˷����� �����⣬ͼ��ÿ���߶α�ʾ���߶����˵��һ��ֱ�ߣ�
���㣬5 ���㣬����n ���㣬���������� ���㶼����ͬһ��ֱ����.����ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ� �� ̽����Ϊ�˽��������⣬ϣ��С���ͬѧ����������±������̽������Ϊ�˷����� �����⣬ͼ��ÿ���߶α�ʾ���߶����˵��һ��ֱ�ߣ�
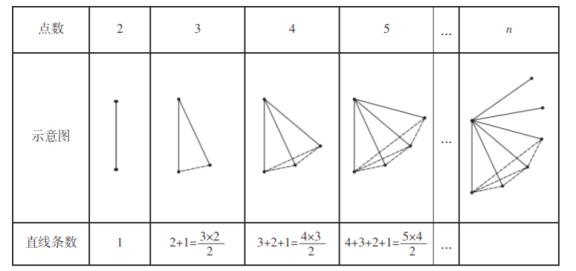
�����������⣺
��1�������ϣ��С����ɣ���ֱ��д�����ۣ���ƽ������![]() ����ʱ��ֱ������Ϊ ��
����ʱ��ֱ������Ϊ ��
��2����ijͬѧ���ձ����еķ�����������![]() ��ֱ�ߣ����ƽ�����ж��ٸ���֪��.
��ֱ�ߣ����ƽ�����ж��ٸ���֪��.
���𰸡���1��![]() ����2��8.
����2��8.
��������
��1�����ݹ������ֱ����1����������ͬһֱ���ϵ������ֱ����3�������κ����㶼����һ��ֱ�����ĵ��ֱ����6�������˹��ɣ������һ�㣬�ܽ����ʽ��![]() ����2����28���빫ʽ��n����.
����2����28���빫ʽ��n����.
�⣺��1����ƽ������2����ʱ�����Ի�![]() ��ֱ�ߣ�
��ֱ�ߣ�
��ƽ������3����ʱ�����Ի�![]() ��ֱ�ߣ�
��ֱ�ߣ�
��ƽ������4����ʱ�����Ի�![]() ��ֱ�ߣ�
��ֱ�ߣ�
��
��ƽ������n��n��2������ʱ�����Ի�![]() ��ֱ�ߣ�
��ֱ�ߣ�
![]() ���ƽ������
���ƽ������ ![]() ����֪��.
����֪��.
�����⣬��![]()
���![]() ���ᣩ
���ᣩ
�𣺸�ƽ������![]() ����֪��
����֪��


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С���ڽ�ѧ¥A���ֱ�۲����ʵ��¥CD�ײ��ĸ���Ϊ45��������������Ϊ37������֪��ѧ¥��ʵ��¥��ͬһƽ���ϣ��۲������Ĵ�ֱ�߶�ABΪ15m����ʵ��¥�Ĵ�ֱ�߶ȼ�CD������ȷ��1m����
�ο�ֵ��sin37��=0.60��cos37��=0.80��tan37��=0.75��
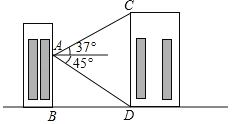
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ�
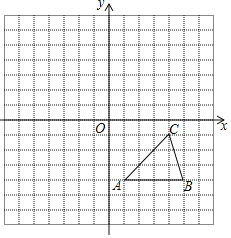
��1������ABC����ƽ��5����λ��õ���Ӧ����A1B1C1��������A1B1C1��
��2����������ABC����ԭ��O�ԳƵ���A2B2C2��
��3����A1B1C1����A2B2C2����ij����Գƣ�������������Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�鷽�̣���![]() ����
����![]() ����
����![]() ����С��ͨ���۲죬�����������̺��Ĺ��ɣ���˳���������ǰ�������̵Ľ�ڢٸ����̵Ľ�Ϊ
����С��ͨ���۲죬�����������̺��Ĺ��ɣ���˳���������ǰ�������̵Ľ�ڢٸ����̵Ľ�Ϊ![]() ���ڢڸ����̵Ľ�Ϊ
���ڢڸ����̵Ľ�Ϊ![]() ���ڢ۸����̵Ľ�Ϊ
���ڢ۸����̵Ľ�Ϊ![]() .��nΪ���������ҹ���x�ķ���
.��nΪ���������ҹ���x�ķ���![]() ��һ������
��һ������![]() ����n��ֵ����____________.
����n��ֵ����____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y1��x+m��ͼ����x��y��ֱ��ڵ�A��B���뷴��������y2��![]() ��x��0����ͼ��ֱ��ڵ�C��D����C�������Ϊ����1��2����
��x��0����ͼ��ֱ��ڵ�C��D����C�������Ϊ����1��2����
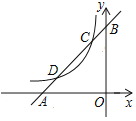
��1���ֱ����һ�κ����������������Ĺ�ϵʽ��
��2�������D�����겢ֱ��д��y1��y2�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ���ھƣ��ֳơ��ӻ���ơ�.����ھ���ѡ�ý���ƽԭ�ġ�һ��ץ������Ϊԭ��.������ij���������2016����ֲ��һ��ץ������100Ķ��2018��ú����������ˡ�һ��ץ����������ֲ���������ֲ144Ķ.
��1����ú�������������ֲ��һ��ץ������Ķ����ƽ�������ʣ�
��2��ij�������ۡ�һ��ץ�������ۼ�Ϊ13Ԫ/�ÿ����۳�30�ÿ���ӯ����1.5Ԫ.Ϊ�˼��ٿ�棬�������������.�������з��֣��ۼ�ÿ����0.1Ԫ����ɶ��۳�2��.��������ij�����ۡ�һ��ץ��������ӯ��Ϊ40Ԫ����õ굱�����۵��۽����˶���Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ��������������ֱ�Ϊ
��������������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��ÿ������ı߳���Ϊ1����λ���ȣ�.
��ÿ������ı߳���Ϊ1����λ���ȣ�.
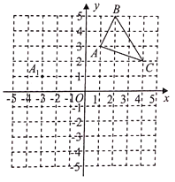
��1����![]() ƽ�ƣ�ʹ��
ƽ�ƣ�ʹ��![]() �ƶ�����
�ƶ�����![]() ���뻭��
���뻭��![]() ��
��
��2������![]() ����
����![]() ������ĶԳƵ�
������ĶԳƵ�![]() ����ֱ��д��
����ֱ��д��![]() ��
��![]() ��
��![]() �����ꣻ
�����ꣻ
��3��![]() ��
��![]() �Ƿ�����ĶԳƣ����ǣ���д���Գ����ĵ����ꣻ�����ǣ���˵������.
�Ƿ�����ĶԳƣ����ǣ���д���Գ����ĵ����ꣻ�����ǣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ��ͼ����ֱ��y=kx+b�ཻ�ڵ�A��B����A������Ϊ(2��4)��ֱ��AB��y���ڵ�C(0��2)����x���ڵ�E.
��ͼ����ֱ��y=kx+b�ཻ�ڵ�A��B����A������Ϊ(2��4)��ֱ��AB��y���ڵ�C(0��2)����x���ڵ�E.
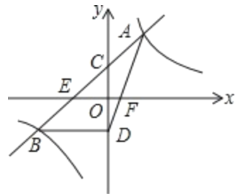
(1)����������һ�κ����ı���ʽ;
(2)���E��B������;
(3)����B��BD��y�ᣬ����ΪD������AD��x���ڵ�F����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y��ax2��4ax+b������A��1��0������x�ύ�ڵ�B����y�ύ�ڵ�C����OB��OC��
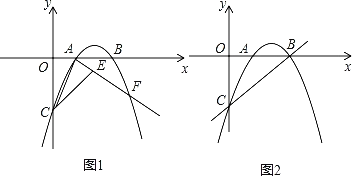
��1���������ߵĽ���ʽ��
��2������OAC��AC���۵õ���ACE��ֱ��AE���������ڵ�P�����P�����ꣻ
��3����ͼ2����MΪֱ��BC��һ�㣨����B��C�غϣ�����OM����OM��O����ת90�����õ��߶�ON���Ƿ���������ĵ�N��ʹ��Nǡ�����������ϣ������ڣ������N�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com