
科目:初中数学 来源: 题型:
| 品牌 | A | B |
| 成本价(万元/台) | 3 | 5 |
| 销售价(万元/台) | 4 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
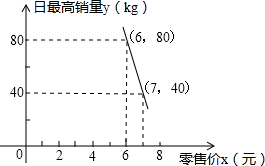 某水果经销商到水果批发市场批发某种水果时了解到如下行情:每千克水果的批发价为4元,经调查,经销商销售该水果的日最高销量与零售价之间的函数关系如图中直线AB所示,该经销商准备购进一定量的水果,且在销售时当日零售价保持不变,考虑到保鲜水果要增加成本,因此经销商要确保每天批发进来的水果全部售完.
某水果经销商到水果批发市场批发某种水果时了解到如下行情:每千克水果的批发价为4元,经调查,经销商销售该水果的日最高销量与零售价之间的函数关系如图中直线AB所示,该经销商准备购进一定量的水果,且在销售时当日零售价保持不变,考虑到保鲜水果要增加成本,因此经销商要确保每天批发进来的水果全部售完.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com