
分析 (1)在平面直角坐标系内描出点(0,-4)和(-3,0),画出一次函数的图象即可;
(2)把点(0,-4)和(-3,0)代入直线y=kx+b求出k、b的值即可得出直线的解析式;
(3)求出C点的坐标,根据勾股定理求得AB,即可BC,从而求得△ABC的面积与周长.
解答 解:(1)其图象如图所示: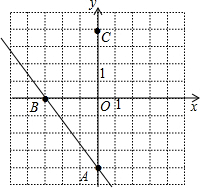
(2)∵直线与y轴交于点A(0,-4),与x轴交于点B(-3,0).
设直线y=kx+b,
∴$\left\{\begin{array}{l}{b=-4}\\{-3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-4}\end{array}\right.$,
∴直线的解析式为:y=$\frac{4}{3}$x-4;
(3)∵A(0,-4),B(-3,0),
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵点C与点A关于x轴对称,
∴C(0,4),
∴AC=4+4=8,BC=AB=5,
∴△ABC的面积=$\frac{1}{2}$AC•OB=$\frac{1}{2}×8×3$=12,
△ABC的周长=5+5+8=18.
点评 本题考查的是用待定系数法求一次函数的解析式及一次函数的性质,熟知用待定系数法求一次函数的解析式的基本步骤是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y1>y3>y2 | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2=4 | B. | (x-3)2=14 | C. | (x+3)2=4 | D. | (x+3)2=14 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某计算机中有
如图,某计算机中有 、
、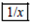 、
、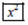 三个按键,以下是这三个按键的功能.
三个按键,以下是这三个按键的功能. :将荧幕显示的数变成它的正平方根,例如:荧幕显示的数为49时,按下
:将荧幕显示的数变成它的正平方根,例如:荧幕显示的数为49时,按下 后会变成7.
后会变成7.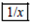 :将荧幕显示的数变成它的倒数,例如:荧幕显示的数为25时,按下
:将荧幕显示的数变成它的倒数,例如:荧幕显示的数为25时,按下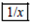 后会变成0.04.
后会变成0.04.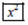 :将荧幕显示的数变成它的平方,例如:荧幕显示的数为6时,按下
:将荧幕显示的数变成它的平方,例如:荧幕显示的数为6时,按下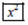 后会变成36.
后会变成36. ,第二下按
,第二下按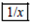 ,第三下按
,第三下按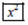 ,之后以
,之后以 、
、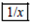 、
、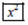 的顺序轮流按,则当他按了第100下后荧幕显示的数是多少( )
的顺序轮流按,则当他按了第100下后荧幕显示的数是多少( )| A. | 0.01 | B. | 0.1 | C. | 10 | D. | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com