
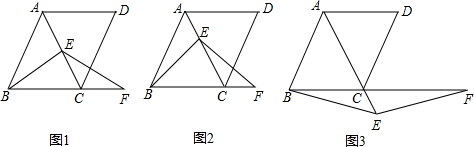

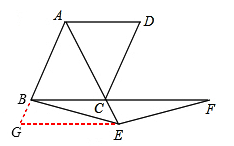
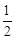 ∠ABC=30°,AE=CE,所以CE=CF,然后等边对等角的性质可得∠F=∠CEF,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠F=30°,从而得到∠CBE=∠F,根据等角对等边的性质即可证明。
∠ABC=30°,AE=CE,所以CE=CF,然后等边对等角的性质可得∠F=∠CEF,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠F=30°,从而得到∠CBE=∠F,根据等角对等边的性质即可证明。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:单选题

| A.6cm | B.8cm | C.10cm | D.12cm |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).
ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).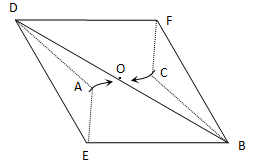
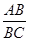 的值.
的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的直角梯形,上底长为10cm,与底垂直的腰长为10cm,以上底或与底垂直的腰为一边作三角形,使三角形的另一边长为15cm,第三个顶点落在下底上.请计算所作的三角形的面积.
的直角梯形,上底长为10cm,与底垂直的腰长为10cm,以上底或与底垂直的腰为一边作三角形,使三角形的另一边长为15cm,第三个顶点落在下底上.请计算所作的三角形的面积.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
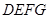 的边
的边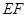 在
在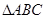 的边
的边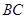 上,顶点
上,顶点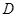 、
、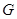 分别在边
分别在边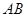 、
、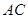 上,
上,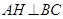 ,垂足为
,垂足为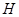 .已知
.已知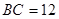 ,
,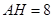 .
.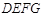 为正方形时,求该正方形的边长;
为正方形时,求该正方形的边长;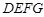 面积为18时,求矩形的长和宽.
面积为18时,求矩形的长和宽.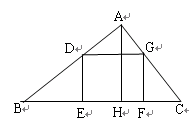
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com