


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:022
如图,⊙O1,⊙O2相交于点A、B,现给出四个命题:
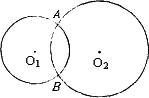
(1)若AC是⊙O2的切线且交⊙O1于点C,AD是⊙O1的切线且交⊙O2于点D,则AB2=BC·BD.
(2)连接AB、O1O2,若O1A=15 cm,O2A=20 cm,AB=24 cm,则O1O2=25 cm.
(3)若CA是⊙O1的直径,DA是⊙O2的一条非直径的弦,且点D、B不重合,则C、B、D三点不在同一直线上.
(4)若过点A作⊙O1的切线交⊙O2于点D,直线DB交⊙O1于点C,直线CA交⊙O2于点E,连DE,则DE2=DB·DC.
则正确命题的序号是________(在横线上填上所有正确命题序号).
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:新课标九年级数学竞赛培训第05讲:一元二次方程的整数解(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com