
【题目】已知抛物线![]() 的顶点为
的顶点为![]() ,经过原点
,经过原点![]() 且与
且与![]() 轴另一交点为
轴另一交点为![]() .
.
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 若
若![]() 为等腰直角三角形,求抛物线
为等腰直角三角形,求抛物线![]() 的解析式;
的解析式;
![]() 现将抛物线
现将抛物线![]() 绕着点
绕着点![]() 旋转
旋转![]() 后得到抛物线
后得到抛物线![]() ,若抛物线
,若抛物线![]() 的顶点为
的顶点为![]() ,当
,当![]() ,且顶点
,且顶点![]() 在抛物线
在抛物线![]() 上时,求
上时,求![]() 的值.
的值.
【答案】![]() ;
;![]() 抛物线
抛物线![]() ;
;![]() 或
或![]() .
.
【解析】
(1)由抛物线经过原点可知当x=0时,y=0,由此可得关于x的一元二次方程,解方程即可求出抛物线x轴另一交点坐标;
(2)由△AMO为等腰直角三角形,抛物线的顶点为M,可求出b的值,再把原点坐标(0,0)代入求出a的值,即可求出抛物线C1的解析式;
(3)由b=1,易求线抛物线C1的解析式,设N(n,-1),再由点P(m,0)可求出n和m的关系,当顶点N在抛物线C1上可把N的坐标代入抛物线即可求出m的值.
![]() ∵抛物线
∵抛物线![]() 经过原点
经过原点![]() ,
,
∴![]() ,
,
∴当![]() 时,则
时,则![]() ,
,
解得:![]() 或
或![]() ,
,
∴抛物线与![]() 轴另一交点
轴另一交点![]() 坐标是
坐标是![]() ;
;
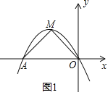
![]() ∵抛物线
∵抛物线![]() ,(如图
,(如图![]() )
)
∴顶点![]() 坐标为
坐标为![]() ,
,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∵抛物线![]() 过原点,
过原点,
∴![]() ,
,
解得:![]() ,
,
∴抛物线![]() ;
;
![]() ∵
∵![]() ,抛物线
,抛物线![]() 过原点,
过原点,
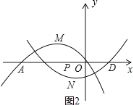
(如图![]() )
)
∴![]() ,
,
∴![]() ,
,
设![]() ,又因为点
,又因为点![]() ,
,
∴![]() ,
,
∴![]()
即点![]() 的坐标是
的坐标是![]() ,
,
∵顶点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,
,
解得:![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
小聪观察上表,得出下面结论:①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ;②函数
;②函数![]() 的最大值为
的最大值为![]() ;③抛物线的对称轴是
;③抛物线的对称轴是![]() ;④在对称轴左侧,
;④在对称轴左侧,![]() 随
随![]() 增大而增大.其中正确有( )
增大而增大.其中正确有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某大学的楼门是一抛物线形水泥建筑物,大门的地面宽度为![]() ,两侧距离地面
,两侧距离地面![]() 高处各有一个挂校名横匾用的铁环,两铁环的水平距离为
高处各有一个挂校名横匾用的铁环,两铁环的水平距离为![]() ,则校门的高约为(精确到
,则校门的高约为(精确到![]() ,水泥建筑物的厚度忽略不计)( )
,水泥建筑物的厚度忽略不计)( )
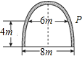
A. 9.2m B. 9.1m C. 9.0m D. 8.9m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3),B(-3,2),C(-1,1).

(1)若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;
(2)画出△A1B1C1绕原点旋转180°后得到的△A2B2C2;
(3)△A'B'C'与△ABC是位似图形,请写出位似中心的坐标:______;
(4)顺次连接C,C1,C',C2,所得到的图形是轴对称图形吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知MN∥EF∥BC,点A、D为直线MN上的两动点,AD=a,BC=b,AE∶ED=m∶n;
(1)当点A、D重合,即a=0时(如图1),试求EF.(用含m,n,b的代数式表示)
(2)请直接应用(1)的结论解决下面问题:当A、D不重合,即a≠0,
①如图2这种情况时,试求EF.(用含a,b,m,n的代数式表示)
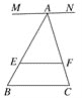
图1
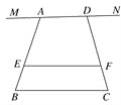
图2
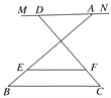
图3
②如图3这种情况时,试猜想EF与a、b之间有何种数量关系?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断不正确的是( )
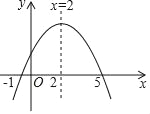
A. ac<0 B. a﹣b+c>0 C. b=﹣4a D. a+b+c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com