
【题目】居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.
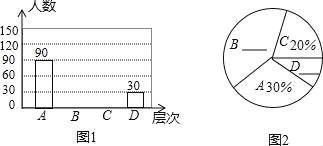
请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
【答案】(1)本次被抽查的居民有300人;
(2)
(3)该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有2800人.
【解析】
试题分析:(1)由被调查人数=A层次的人数÷A层次人数占被调查人数的百分比,计算可得;
(2)根据D层次人数÷被调查总人数=D层次百分比,用1减去其它层次百分比可得B层次百分比,将B、C两层次百分比分别乘以被调查总人数可得B、C层次的人数,补全图形;
(3)用A、B两层次百分比之和乘以总人数4000可得.
试题解析:(1)∵90÷30%=300(人),
∴本次被抽查的居民有300人.
(2)∵D所占的百分比:30÷300=10%,
∴B所占的百分比:1﹣20%﹣30%﹣10%=40%,
∴B对应的人数:300×40%=120(人),C对应的人数:300×20%=60(人),
补全统计图,如图所示:

(3)∵4000×(30%+40%)=2800(人),
∴估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有2800人.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
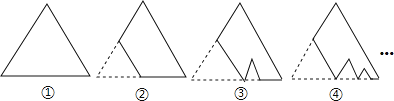
【题目】如图,图①是一块边长为1,周长记为P1的等边三角形纸板,沿图①的底边剪去一块边长的![]() 的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() )后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________
)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.
(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?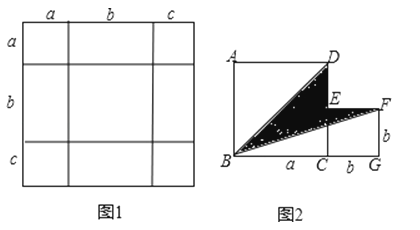
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表为宁波市2016年4月上旬10天的日最低气温情况,则这10天中日最低气温的中位数和众数分别是( )
温度(℃) | 11 | 13 | 14 | 15 | 16 |
天数 | 1 | 5 | 2 | 1 | 1 |
A.14℃,14℃
B.14℃,13℃
C.13℃,13℃
D.13℃,14℃
查看答案和解析>>
科目:初中数学 来源: 题型:
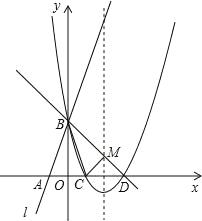
【题目】如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在同一年出生的400人中至少有两人的生日相同
B.投掷一粒骰子,连投两次点数相同的概率与连投两次点数都为1的概率是相等的
C.从一副完整的扑克牌中随机抽取一张牌恰好是红桃K,这是必然事件
D.一个袋中装有3个红球,5个白球,任意摸出一个球是红球的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接省运会在我市召开,市里组织了一个梯形鲜花队参加开幕式,要求共站60排,第一排40人,后面每一排都比前一排都多站一人,则每排人数y与该排排数x之间的函数关系式为____(x为1≤x≤60的整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com