
 (2013•丰台区一模)我们把函数图象与x轴交点的横坐标称为这个函数的零点.如函数y=2x+1的图象与x轴交点的坐标为(-
(2013•丰台区一模)我们把函数图象与x轴交点的横坐标称为这个函数的零点.如函数y=2x+1的图象与x轴交点的坐标为(-| 1 |
| 2 |
| 1 |
| 2 |
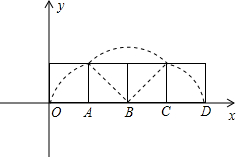 解得x=-5或1.
解得x=-5或1.| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 (2013•丰台区一模)如图,四边形ABCD中,AB=AD,∠BAD=90°,∠CBD=30°,∠BCD=45°,若AB=2
(2013•丰台区一模)如图,四边形ABCD中,AB=AD,∠BAD=90°,∠CBD=30°,∠BCD=45°,若AB=2| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| 电器 | 彩电 | 洗衣机 | 冰箱 |
| 前5天的销售总量(台) | 150 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
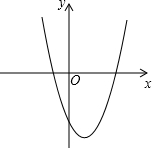 (2013•丰台区一模)二次函数y=x2+bx+c的图象如图所示,其顶点坐标为M(1,-4).
(2013•丰台区一模)二次函数y=x2+bx+c的图象如图所示,其顶点坐标为M(1,-4).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•丰台区一模)如图,在平面直角坐标系xOy中,⊙C的圆心坐标为(-2,-2),半径为
(2013•丰台区一模)如图,在平面直角坐标系xOy中,⊙C的圆心坐标为(-2,-2),半径为| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com