
分析 (1)根据所给出的等式找出规律,即可得出第n个算式;
(2)根据(1)得出的规律解答即可.
解答 解:(1)第n个等式为:$\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$;
(2)$\frac{1}{1×3}+\frac{1}{3×5}+\frac{1}{5×7}+…\frac{1}{2015×2017}$
=$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+\frac{1}{2015}-\frac{1}{2017})$
=$\frac{1}{2}(1-\frac{1}{2017})$
=$\frac{1008}{2017}$.
点评 此题考查数字的变化规律,发现规律,利用规律解决问题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
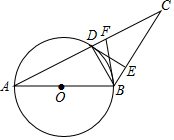 如图,在⊙O中,直径AB=8,∠A=30°,AC=8$\sqrt{3}$,AC与⊙O交于点D.
如图,在⊙O中,直径AB=8,∠A=30°,AC=8$\sqrt{3}$,AC与⊙O交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
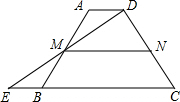 如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.
如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com