

 CF,
CF, CH·CG=
CH·CG= ×
× CF×CG=
CF×CG= CG·CG=6(cm2),
CG·CG=6(cm2), (CF+AB)·BC=
(CF+AB)·BC= CF·BC+
CF·BC+ AB·BC=
AB·BC= CG·AB+
CG·AB+ AB·BC
AB·BC AB·(CG+BC)
AB·(CG+BC) HF·AD=
HF·AD= CG·CH,
CG·CH, (CF-CH)·AD=
(CF-CH)·AD= CG·CH,
CG·CH,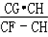 =
=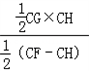 =
=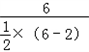 =3(cm),
=3(cm), (AB+CF)·BC=
(AB+CF)·BC= ×(3+6)×3=13.5(cm2),
×(3+6)×3=13.5(cm2),

科目:初中数学 来源: 题型:
 如图,在矩形ABCD中,AD=5,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于
如图,在矩形ABCD中,AD=5,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏灌南实验中学九年级第一次阶段性检测数学试卷(带解析) 题型:解答题
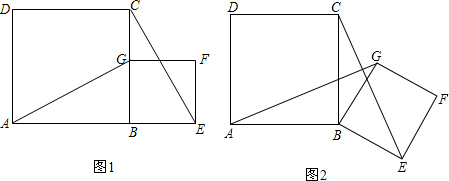
如图正方形ABCD和正方形EFGH,F和B重合,EF在AB上,连DH(本题14分)
⑴、由图⑴易知,
①线段AE=CG, AE和CG所在直线互相垂直,且此时易求得② 。
。
⑵、若把正方形EFGH绕F点逆时针旋转 度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
⑶、若把图⑴中的正方形EFGH沿BD方向以每秒1cm的速度平移,设平移时间为x秒,正方形ABCD和正方形EFGH的边长分别为5cm和1cm,
①在平移过程中,△AFH是否会成为等腰三角形?若能求出x的值,若不能,说明理由.
②在平移过程中,△AFH是否会成为等边三角形?若能求出x的值,若不能,设正方形ABCD和正方形EFGH的边长分别为acm和bcm,则当a、b满足什么关系时,△AFH可以成为等边三角形.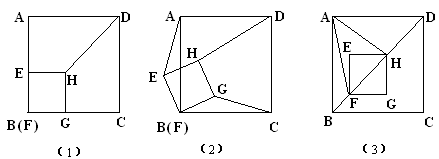
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏灌南实验中学九年级第一次阶段性检测数学试卷(解析版) 题型:解答题
如图正方形ABCD和正方形EFGH,F和B重合,EF在AB上,连DH(本题14分)
⑴、由图⑴易知,
①线段AE=CG, AE和CG所在直线互相垂直,且此时易求得② 。
。
⑵、若把正方形EFGH绕F点逆时针旋转 度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
⑶、若把图⑴中的正方形EFGH沿BD方向以每秒1cm的速度平移,设平移时间为x秒,正方形ABCD和正方形EFGH的边长分别为5cm和1cm,
①在平移过程中,△AFH是否会成为等腰三角形?若能求出x的值,若不能,说明理由.
②在平移过程中,△AFH是否会成为等边三角形?若能求出x的值,若不能,设正方形ABCD和正方形EFGH的边长分别为acm和bcm,则当a、b满足什么关系时,△AFH可以成为等边三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com