
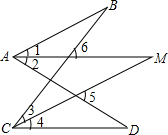
 已知∠B=32°,∠D=38°,AM,CM分别平分∠BAD和∠BCD,求∠M的大小.
已知∠B=32°,∠D=38°,AM,CM分别平分∠BAD和∠BCD,求∠M的大小.| 1 |
| 2 |
| 1 |
| 2 |


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
 如图,用两个转盘进行“配绿色”游戏(黄色和蓝色配在一起为绿色),同时转动两个转盘,当转盘停止转动时,用两盘指针所指的颜色配色,求能配出绿色的概率(用树形图或列表法表示).
如图,用两个转盘进行“配绿色”游戏(黄色和蓝色配在一起为绿色),同时转动两个转盘,当转盘停止转动时,用两盘指针所指的颜色配色,求能配出绿色的概率(用树形图或列表法表示).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知,B(-1,0)、C(0,3)、P(-2,-1),M(-2.5,1.5),若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.
如图,已知,B(-1,0)、C(0,3)、P(-2,-1),M(-2.5,1.5),若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com