
 已知y=x2+2x+c与x轴交于A,B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(-3,0).
已知y=x2+2x+c与x轴交于A,B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(-3,0).分析 (1)将点A的坐标代入到抛物线的解析式求得c值,然后配方后即可确定点C,点D的坐标;
(2)连结AC,CD,根据勾股定理的逆定理可求∠ACD=90°,取AD中点O′,连结O′C,可得O′C=$\frac{1}{2}$AD,再根据点与圆的位置关系即可求解;
(3)根据相似三角形的判定可得△OBC∽△CDA,根据相似三角形的性质可得∠OCB=∠CAD,进一步可求∠E=45°;
(4)作抛物线的对称轴交x轴于点H,设直线PQ交y轴于点N.根据AA可得△PON∽△DHA,根据相似三角形的性质可得N(0,2),可得直线PQ的解析式,联立抛物线解析式即可得到点Q的坐标.
解答 解:(1)∵A(-3,0),
∴9-6+c=0,
解得c=-3,
即y=x2+2x-3=(x+1)2-4,
∴C(0,-3),D(-1,-4);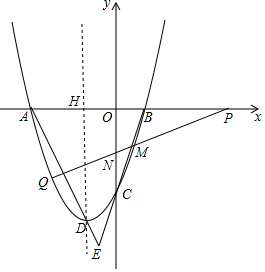 (2)连结AC,CD,
(2)连结AC,CD,
∵AC=3$\sqrt{2}$,AD=2$\sqrt{5}$,CD=$\sqrt{2}$,
AC2+CD2=AD2,
∴∠ACD=90°,
取AD中点O′,连结O′C,则O′C=$\frac{1}{2}$AD,
∴点C在以AD为直径的圆上;
(3)∵OA=3,OB=1,AC=3$\sqrt{2}$,CD=$\sqrt{2}$,
∴$\frac{OB}{CD}$=$\frac{OC}{AC}$=$\frac{1}{\sqrt{2}}$,
又∵∠BOC=∠ACD=90°,
∴△OBC∽△CDA,
∴∠OCB=∠CAD,
又∵∠ACB=45°+∠OCB=∠E+∠CAD,
∴∠E=45°;
(4)作抛物线的对称轴交x轴于点H,设直线PQ交y轴于点N.
∵∠PMB=∠E=45°,
∴PQ⊥AD,
∴∠ADH=∠APM,
又∵∠PON=∠AHD=90°,
∴△PON∽△DHA,
∴$\frac{OP}{DH}$=$\frac{ON}{AH}$,即$\frac{4}{4}$=$\frac{ON}{2}$,
∴ON=2,即N(0,2),
∴yPQ=$\frac{1}{2}$x-2,
∴$\left\{\begin{array}{l}{y=\frac{1}{2}x-2}\\{y={x}^{2}+2x-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=-3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{1}{2}}\\{{y}_{2}=-\frac{7}{4}}\end{array}\right.$.
即:Q(-2,-3)或Q($\frac{1}{2}$,-$\frac{7}{4}$).
点评 本题考查了二次函数的综合知识,难度较大,题目中渗透了许多的知识点,特别是二次函数与相似三角形的结合,更是一个难点,同时也是中考中的常考题型之一.


科目:初中数学 来源: 题型:填空题
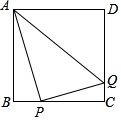 如图,正方形ABCD的边长为4,点P为BC边上的动点,连接AP,作PQ⊥AP,交CD于点Q,连接AQ,当点P从B点运动到C点时,线段AQ的中点所经过的路径长为1.
如图,正方形ABCD的边长为4,点P为BC边上的动点,连接AP,作PQ⊥AP,交CD于点Q,连接AQ,当点P从B点运动到C点时,线段AQ的中点所经过的路径长为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com