Question

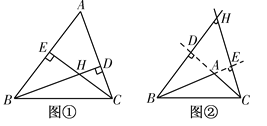
【题目】（1）如图①，△ABC是锐角三角形，高BD，CE相交于点H，找出∠BHC和∠A之间存在何种等量关系；并证明你的结论；

（2）如图②，若△ABC是钝角三角形，∠A＞90°，高BD，CE所在的直线相交于点H，请你判断此时（1）中的等量关系是否仍然成立？并说明理由．

Answer 1

【答案】（1）∠BHC＝180-∠A；（2）∠BHC＝180-∠A．

【解析】试题分析：⑴由题易得∠ A+∠ ACE=90°，∠ ACE+∠DHC=90°，所以∠ A=∠ DHC，由图可知，∠ DHC与∠ BHC互补，故∠ A与∠ BHC互补.

⑵由⑴可知，∠BHC=∠ EAC，由图可知，∠ EAC与∠ BAC互补，所以∠ BHC与∠ BAC互补，故⑴中结论仍然成立.

试题解析：（1）∵BD⊥ AC ， ∴ ∠ ADB＝90°.

∵ CE⊥ AB ， ∴∠ AEC＝90°.

∵∠ A+∠ ADB+∠ AEC+∠ DHE＝360°，

∴∠ DHE＝ 360°-（∠ A+∠ ADB+∠ AEC）＝360°-（∠ A+90°+90°）＝180°-∠ A，

∴ ∠ BHC＝∠ DHE＝180°-∠ A.

（2） ∵ BD⊥ AC ，∴ ∠ ADH＝90°.

∵ CE⊥ AB ， ∴ ∠ AEH＝90°.

∵ ∠ DAE+∠ ADH+∠ AEH+∠ BHC＝360°，

∴ ∠ BHC＝360°-（∠ DAE+∠ ADH+∠ AEH）＝360°-（∠ DAE+90°+90°）＝180°-∠ DAE，

∴ ∠ BHC＝180°-∠ A.