

分析 (1)①利用正方形的性质得△ABD为等腰直角三角形,则BF=$\sqrt{2}$AB,再证明△BEF为等腰直角三角形得到BF=$\sqrt{2}$BE,所以BD-BF=$\sqrt{2}$AB-$\sqrt{2}$BE,从而得到DF=$\sqrt{2}$AE;
②利用旋转的性质得∠ABE=∠DBF,加上$\frac{BF}{BE}$=$\frac{BD}{AB}$=$\sqrt{2}$,则根据相似三角形的判定可得到△ABE∽△DBF,所以$\frac{DF}{AE}$=$\frac{BF}{BE}$=$\sqrt{2}$;
(2)先画出图形得到图3,利用勾股定理得到BD=$\sqrt{1+{m}^{2}}$AB,再证明△BEF∽△BAD得到$\frac{BE}{BA}$=$\frac{BF}{BD}$,则$\frac{BF}{BE}$=$\frac{BD}{BA}$=$\sqrt{1+{m}^{2}}$,接着利用旋转的性质得∠ABE′=∠DBF′,BE′=BE,BF′=BF,所以$\frac{BF′}{BE′}$=$\frac{BD}{BA}$=$\sqrt{1+{m}^{2}}$,然后根据相似三角形的判定方法得到△ABE′∽△DBF′,再利用相似的性质可得$\frac{DF′}{AE′}$=$\frac{BD}{BA}$=$\sqrt{1+{m}^{2}}$.
解答 解:(1)①∵四边形ABCD为正方形,
∴△ABD为等腰直角三角形,
∴BF=$\sqrt{2}$AB,
∵EF⊥AB,
∴△BEF为等腰直角三角形,
BF=$\sqrt{2}$BE,
∴BD-BF=$\sqrt{2}$AB-$\sqrt{2}$BE,
即DF=$\sqrt{2}$AE;
故答案为DF=$\sqrt{2}$AE;
②DF=$\sqrt{2}$AE.理由如下:
∵△EBF绕点B逆时针旋转到图2所示的位置,
∴∠ABE=∠DBF,
∵$\frac{BF}{BE}$=$\sqrt{2}$,$\frac{BD}{AB}$=$\sqrt{2}$,
∴$\frac{BF}{BE}$=$\frac{BD}{AB}$,
∴△ABE∽△DBF,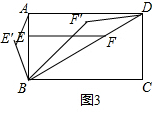
∴$\frac{DF}{AE}$=$\frac{BF}{BE}$=$\sqrt{2}$,
即DF=$\sqrt{2}$AE;
(2)如图3,∵四边形ABCD为矩形,
∴AD=BC=mAB,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{1+{m}^{2}}$AB,
∵EF⊥AB,
∴EF∥AD,
∴△BEF∽△BAD,
∴$\frac{BE}{BA}$=$\frac{BF}{BD}$,
∴$\frac{BF}{BE}$=$\frac{BD}{BA}$=$\sqrt{1+{m}^{2}}$,
∵△EBF绕点B顺时针旋转α(0°<α<90°)得到△E'BF',
∴∠ABE′=∠DBF′,BE′=BE,BF′=BF,
∴$\frac{BF′}{BE′}$=$\frac{BD}{BA}$=$\sqrt{1+{m}^{2}}$,
∴△ABE′∽△DBF′,
∴$\frac{DF′}{AE′}$=$\frac{BD}{BA}$=$\sqrt{1+{m}^{2}}$,
即DF′=$\sqrt{1+{m}^{2}}$AE′.
点评 本题考查了相似形的综合题:熟练掌握旋转的性质、矩形和正方形的性质;灵活应用相似三角形的判定和性质,会利用相似比表示线段之间的关系.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 月用水量/m3 | 4 | 5 | 6 | 8 | 9 | 10 |
| 户数 | 6 | 7 | 9 | 5 | 2 | 1 |
| A. | 6,6 | B. | 9,6 | C. | 9,6 | D. | 6,7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 鸡的质量/kg | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 烤制时间/min | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com