
【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.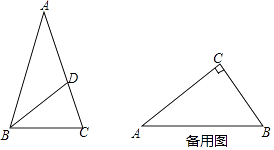
(1)等边三角形“內似线”的条数为;
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长.
【答案】
(1)3
(2)证明:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD,
∴△BCD∽△ABC,
又∵∠BDC=∠A+∠ABD,
∴∠ABD=∠CBD,
∴BD平分∠ABC,
即BD过△ABC的内心,
∴BD是△ABC的“內似线”;
(3)解:设D是△ABC的内心,连接CD,
则CD平分∠ACB,
∵EF是△ABC的“內似线”,
∴△CEF与△ABC相似;
分两种情况:①当 ![]() =
= ![]() =
= ![]() 时,EF∥AB,
时,EF∥AB,
∵∠ACB=90°,AC=4,BC=3,
∴AB= ![]() =5,
=5,
作DN⊥BC于N,如图2所示:
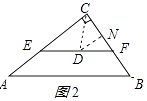
则DN∥AC,DN是Rt△ABC的内切圆半径,
∴DN= ![]() (AC+BC﹣AB)=1,
(AC+BC﹣AB)=1,
∵CD平分∠ACB,
∴ ![]() =
= ![]() ,
,
∵DN∥AC,
∴ ![]() =
= ![]() ,即
,即 ![]() ,
,
∴CE= ![]() ,
,
∵EF∥AB,
∴△CEF∽△CAB,
∴ ![]() ,即
,即 ![]() ,
,
解得:EF= ![]() ;
;
②当 ![]() =
= ![]() =
= ![]() 时,同理得:EF=
时,同理得:EF= ![]() ;
;
综上所述,EF的长为 ![]() .
.
【解析】(1)解:等边三角形“內似线”的条数为3条;理由如下:
过等边三角形的内心分别作三边的平行线,如图1所示:
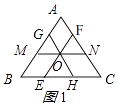
则△AMN∽△ABC,△CEF∽△CBA,△BGH∽△BAC,
∴MN、EF、GH是等边三角形ABC的內似线”;
所以答案是:3.
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为米. (注:不计测量人员的身高,结果按四舍五入保留整数,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A,B两点,AB=18,原点O是线段AB上的一点,OA=2OB.
(1)求出A,B两点所表示的数;
(2)若点C是线段AO上一点,且满足 AC=CO+CB,求C点所表示的数;
(3)若点E以3个单位长度/秒的速度从点A沿数轴向点B方向匀速运动,同时点F以1个单位长度/秒的速度从点B沿数轴向右匀速运动,并设运动时间为t秒,问t为多少时,E、F两点重合.并求出此时数轴上所表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如何求tan75°的值?按下列方法作图可解决问题.如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BM上截取线段BD,使BD=AB,连接AD.连接此图可求得tan75°的值为( )
A.2- ![]()
B.2+ ![]()
C.1+ ![]()
D.![]()
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.

(1)请在图中画出平移后的△ABC
(2)再在图中画出△ABC的高CD
(3)![]() =
=
(4)在右图中能使![]() 的格点P的个数有 个(点P异于A) .
的格点P的个数有 个(点P异于A) .
查看答案和解析>>
科目:初中数学 来源: 题型:
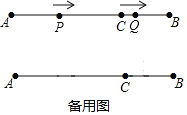
【题目】如图,AB=12cm,点C在线段AB上,AC=3BC,动点P从点A出发,以4cm/s的速度向右运动,到达点B之后立即返回,以4cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动,到达点B之后立即返回,以1cm/s的速度向左运动.设它们同时出发,运动时间为t秒,当第二次重合时,P、Q两点停止运动.
(1)AC=______cm,BC=______cm;
(2)当t=______秒时,点P与点Q第一次重合;当t=______秒时,点P与点Q第二次重合;
(3)当t为何值时,AP=PQ?
查看答案和解析>>
科目:初中数学 来源: 题型:
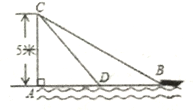
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( )
A. 甲 B. 甲与丁 C. 丙 D. 丙与丁
查看答案和解析>>
科目:初中数学 来源: 题型:
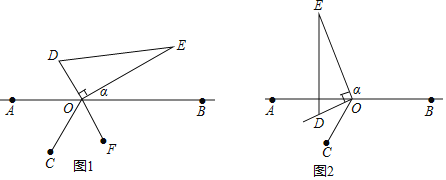
【题目】如图1,点A、O、B在同一直线上,∠AOC=60°,在直线AB另一侧,直角三角形DOE绕直角顶点O逆时针旋转(当OD与OC重合时停止),设∠BOE=α:
(1)如图1,当DO的延长线OF平分∠BOC,∠α=______度;
(2)如图2,若(1)中直角三角形DOE继续逆时针旋转,当OD位于∠AOC的内部,且∠AOD=![]() ∠AOC,∠α=__度;
∠AOC,∠α=__度;
(3)在上述直角三角形DOE的旋转过程中,(∠COD+∠α)的度数是否改变?若不改变,请求出其度数;若改变,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com